Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

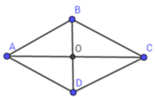
A B C D O
Ta có:
ABCD là hình thoi nên AB = BC = CD = DA ( = CA = 4 cm)
Do đó: tam giác ABC là tam giác đều ( do AB = BC = CA ( = 4 cm))
Suy ra, góc B = 60o
Mà góc B và góc D là hai góc đối nhau nên theo tính chất hình thoi, góc D = 60o
------------------------------------
Theo tính chất hình thoi, 2 đường chéo vuông góc với nhau nên AC vuông góc với BD tại O
Tam giác đều ABC có OB là đường cao nên cũng là đường trung tuyến
Do đó: \(OA=OC=\frac{1}{2}.AC=\frac{1}{2}.4=2\) (cm)
Áp đụng định lý Py-ta-go vào tam giác OAB, ta được:
\(AB^2=OA^2+OB^2\)
\(\Rightarrow\) \(OB^2=AB^2-OA^2=4^2-2^2=16-4=12\)
\(\Rightarrow\) \(OB=\sqrt{12}\) (cm)

Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 20 2 − 16 2 = 12
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.12.16 = 384 (cm2)
Đáp án cần chọn là: A

Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
BO = A B 2 − O A 2 = 10 2 − 6 2 = 8
SABCD = 1 2 BD. AC = 1 2 2OB. 2AO = 2BO. AO = 2.8.6 = 96 (cm2)
Đáp án cần chọn là: B

a: Xét ΔACB và ΔEBC có
\(\widehat{ACB}=\widehat{EBC}\)
BC chung
\(\widehat{ABC}=\widehat{ECB}\)
Do đó: ΔACB=ΔEBC
b: Ta có: ΔACB=ΔEBC
nên AC=EB
=>BE=BD
hay ΔBED cân tại B
c: Ta có: ΔBED cân tại B
nên \(\widehat{BED}=\widehat{BDC}\)
=>\(\widehat{BDC}=\widehat{ACD}\)
d: Xét ΔACD và ΔBDC có
AC=BD
\(\widehat{ACD}=\widehat{BDC}\)
CD chung
DO đó: ΔACD=ΔBDC
e: Ta có: ΔACD=ΔBDC
nên \(\widehat{DAC}=\widehat{DBC}\)
f: Ta có: ΔACD=ΔBDC
nên \(\widehat{ADC}=\widehat{BCD}\)
=>ABCD là hình thang cân