NT
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
PT
1
CM
2 tháng 3 2018
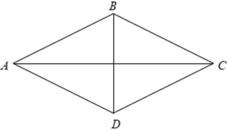
Gọi H là giao điểm của hai đường chéo AC,BD.
⇒ HA = HC = 5( cm )
Áp dụng định lí Py – to – go ta có:
CR
1
26 tháng 3 2020
Kẻ BH vuông góc AD
Tam giác ABH là tam giác đều nên BH=AD=10(cm)
Suy ra SABCD=10.10=100(cm2)
7 tháng 8 2023
1) \(S_{ABCD}=\dfrac{1}{2}.AC.BD\Rightarrow BD=\dfrac{2S_{ABCD}}{AC}=\dfrac{2.50\sqrt[]{3}}{10}=10\sqrt[]{3}\left(cm\right)\)
Gọi O là giao điểm AC và BD
\(\Rightarrow\left\{{}\begin{matrix}OA=\dfrac{1}{2}AC=5\left(cm\right)\\OB=\dfrac{1}{2}BD=5\sqrt[]{3}\left(cm\right)\end{matrix}\right.\)
Xét Δ vuông OAB có :
\(AB^2=OA^2+OC^2=25+25.3=100\left(cm^2\right)\left(Pitago\right)\)
\(\Rightarrow AB=10\left(cm\right)\)
2) Xét Δ vuông OAB có :
\(AB=2OA=10\left(cm\right)\)
⇒ Δ OAB là Δ nửa đều
\(\Rightarrow\left\{{}\begin{matrix}\widehat{ABD}=30^o\\\widehat{BAC}=60^o\end{matrix}\right.\)
mà \(\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2\widehat{BAC}\\\widehat{ADC}=\widehat{ABC}=2\widehat{ABD}\end{matrix}\right.\) (tính chất hình thoi)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{BCD}=\widehat{BAD}=2.60=120^o\\\widehat{ADC}=\widehat{ABC}=2.30=60^o\end{matrix}\right.\)
DT
2
3 tháng 1 2017
Vì: ABCD là hình thoi
=>\(IA=IC=\frac{AC}{2}=\frac{12}{2}=6\)
Xét: \(_{\Delta}\) ABI vuông tại I
=> \(AB^2=AI^2+BI^2\)
=>\(BI^2=AB^2-AI^2=10^2-6^2=64\)
=>BI=8
=>\(BD=2\cdot BI=2\cdot8=16\)
Diện tích hình thoi ABCD là:
\(S_{ABCD}=\frac{1}{2}\cdot AC\cdot BD=\frac{1}{2}\cdot12\cdot16=96\)
3 tháng 1 2017
Không vẽ hình nha.
Xét hình thoi ABCD, có:
AC và BD lần lượt là hai đường chéo của hình thoi ABCD.
Gọi M là giao điểm của hai đường chéo.
=>
\(MA=MC=\frac{AC}{2}=\frac{12}{2}=6\left(cm\right)\)(t/c hình thoi, hai đường chéo cặt nhau tại trung điểm của mỗi đường)
Xét tam giác ABM vuông tại M, có:
AM2 + BM2= AB2 (định lí Py-ta-go)
<=>62+BM2=102
<=>36+BM2=100
=>BM2=100-36
=>BM2=64
=>BM=8(cm)
Theo t/c hình thoi ta lại có:
\(2.MB=BD=2.6=12\left(cm\right)\)
Áp dụng công thức tính diện tích hình thoi ABCD:
Shình thoi ABCD=\(\frac{AC.BD}{2}=\frac{12.16}{2}=96\left(cm^2\right)\)
CM
15 tháng 5 2018
Theo tính chất của hình thoi ta có: O là trung điểm của AC và BD.
Suy ra:
Áp dụng định lí Pytago vào tam giác OAB có:
A B 2 = O A 2 + O B 2 = 6 2 + 10 2 = 136
⇒ A B = 2 34 c m
Chọn đáp án B
CM
28 tháng 8 2017
Ta có: AC = 2AO = 2.12 = 24cm
SABCD = 1 2 BD.AC
=> BD = 2 S A B C D A C = 2.168 24 =14(cm)
=> BO = 1 2 BD = 1 2 .14 = 7(cm)
Áp dụng định lý Py-ta-go trong tam giác vuông AOB vuông tại O ta có:
AB = A O 2 + B O 2 = 12 2 + 7 2 = 193 (cm)
Đáp án cần chọn là: C
Vì : ABCD là hình thoi
\(\Rightarrow IA=IC=\frac{AC}{2}=\frac{12}{2}=6\)
Xét \(\Delta ABI\) vuông tại I
\(\Rightarrow AB^2=AI^2+BI^2\)
\(\Rightarrow BI^2=AB^2-AI^2=10^2-6^2=64\)
\(\Rightarrow BI=8\)
\(\Rightarrow BD=2.BI=2.8=16\)
Diện tích hình thoi ABCD là :
\(S_{ABCD}=\frac{1}{2}.AC.BD=\frac{1}{2}.12.16=96\)
Chúc bạn học tốt !!!