Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Chứng minh được BF = DH \Rightarrow⇒ BFDH là hình bình hành (vì BF // DH). Do đó O thuộc FH (vì O phải là giao điểm của hai đường chéo).
b) Dễ thấy \Delta BEF=\Delta CFGΔBEF=ΔCFG (cgv – cgv) nên EF = FG.
Tương tự, FG = GH, GH = HE \Rightarrow⇒ EF = FG = GH = HE. Suy ra EFGH là hình vuông.
Tương tự phần a) ta chứng minh được O thuộc EG. Từ đó, O là giao điểm hai đường chéo của hình vuông EFGH nên O cách đều E, F, G, H.
c) BE=BC .\cot{{60}^\circ}=\frac{6\sqrt3}{3}=2\sqrt3BE=BC .cot60∘=363=23.
a) Chứng minh được BF = DH \Rightarrow⇒ BFDH là hình bình hành (vì BF // DH). Do đó O thuộc FH (vì O phải là giao điểm của hai đường chéo).
b) Dễ thấy \Delta BEF=\Delta CFGΔBEF=ΔCFG (cgv – cgv) nên EF = FG.
Tương tự, FG = GH, GH = HE \Rightarrow⇒ EF = FG = GH = HE. Suy ra EFGH là hình vuông.
Tương tự phần a) ta chứng minh được O thuộc EG. Từ đó, O là giao điểm hai đường chéo của hình vuông EFGH nên O cách đều E, F, G, H.
c) BE=BC .\cot{{60}^\circ}=\frac{6\sqrt3}{3}=2\sqrt3BE=BC .cot60∘=363=23.

A B C G F E D Q P
a) Ta dễ thấy ^ABF = ^BAF = ^BAD = ^CAD = ^ACE = ^CAE. Suy ra \(\Delta\)ABF ~ \(\Delta\)ACE (g.g) (đpcm).
b) Gọi BE cắt CF tại G. Áp dụng hệ quả ĐL Thales, kết hợp với \(\Delta\)ABF ~ \(\Delta\)ACE ta có:
\(\frac{GC}{GF}=\frac{CE}{FB}=\frac{AC}{AB}\). Mà \(\frac{AC}{AB}=\frac{DC}{DB}\)(ĐL đường phân giác trong tam giác) nên \(\frac{GC}{GF}=\frac{DC}{DB}\)
Do đó GD // BF // CE (ĐL Thales đảo). Lại có AD // BF // CE nên A,G,D thẳng hàng
Vậy thì AD,BE,CF cắt nhau tại G (đpcm).
c) Chú ý GQ // AE suy ra ^AGQ = ^GAE = ^GAF, đồng thời có AG // QF. Suy ra AFQG là hình thang cân (1)
Mặt khác BF // CE dẫn đến ^GFQ = ^GCE = ^GPQ. Từ đây bốn điểm P,Q,F,G cùng thuộc một đường tròn (2)
Từ (1) và (2) suy ra các điểm A,P,G,Q,F cùng thuộc một đường tròn (đpcm).

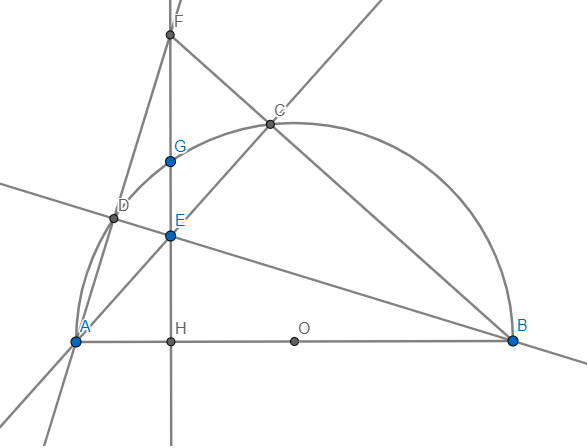
a) Vì AB là đường kính \(\Rightarrow\angle ADB=\angle ACB=90\)
\(\Rightarrow\angle FDE+\angle FCE=90+90=180\Rightarrow ECFD\) nội tiếp
b) GH cắt AD tại F'.F'B cắt AE tại C'
Ta có: \(\left\{{}\begin{matrix}F'H\bot AB\\BD\bot AF'\end{matrix}\right.\Rightarrow E\) là trực tâm \(\Delta F'AB\Rightarrow AE\bot F'B\Rightarrow AC'\bot F'B\)
mà AB là đường kính \(\Rightarrow C'\in\left(O\right)\Rightarrow C\equiv C'\Rightarrow F'\equiv F\Rightarrow\) đpcm

Em tham khảo tại link dưới đây nhé.
Câu hỏi của My Trấn - Toán lớp 9 - Học toán với OnlineMath