Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Do ABCD là hình thang cân nên AD = BC, góc ADH = góc BCK
Xét hai tam giác vuông ADH và BCK ta có:
AD = BC (gt)
góc ADH = góc BCK (gt)
Do đó tam giác ADH = tam giác BCK (cạnh huyền - góc nhọn)
=> HD = KC (hai cạnh tương ứng)
b) Ta có: AH vuông góc CD
BK vuông góc CD
=> AH song song BK
=> Tứ giác ABKH là hình thang
Mặt khác: AH = BK (do tam giác ADH = tam giác BCK)
=> Hình thang ABKH có AB song song HK và AB = HK
=> AB = HK = 6cm
Ta lại có: HK + HD + KC = 15
<=> 6 + 2HD = 15
<=> 2HD = 9
<=> HD = 4,5 (cm)
Vậy HD = KC = 4,5cm
a) Xét tam giác vuông AHD và tam giác BKC có:
^H1 = ^K1= 900 ( gt)
^D =^C ( t/c)
AD = BC ( t/c)
-> tam giác AHD=tam giác BKC( cạnh huyền- góc nhọn)
-> HD=KC ( 2 cạnh tương ứng )
b)
Ta có : AB//CD -> ^ABK =^K1=900 ( 2 góc so le trong)
^AHK=^BKH=900
-> Tứ giác ABKH là HCN ( dhnb)
-> AB=HK =6 (cm)
Mà HD=KC( c/m câu a)
DH+HK+KC=CD=15(cm)
-> 2HD= 15 - 6 = 9 ( cm)
-> HD=KC= 9/ 2 = 4,5 ( cm)

Xét tam giác ADH và tam giác BCK có:
góc AHD= góc BKC
DA= BC (ABCD là hình thang cân)
góc D = góc C (ABCD là htc)
=> tam giác ADH = tam giác BCK (ch-gn)
=> HD = KC (đpcm)

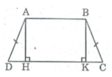
Xét hai tam giác vuông AHD và BKC:
∠ (AHD) = ∠ (BKC) = 90 0
AD = BC (tính chất hình thang cân)
∠ C = ∠ D (gt)
Suy ra: ∆ AHD = ∆ BKC (cạnh huyền, góc nhọn)
⇒ HD = KC


Áp dụng định nghĩa, tính chất và giả thiết của hình thang cân ta có:
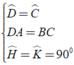
⇒ Δ ADH = Δ BCK
(trường hợp cạnh huyền – góc nhọn)
⇒ DH = CK (cặp cạnh tương ứng bằng nhau)
Vậy DH = CK. (đpcm)
1: Xét ΔAHD vuông tại H và ΔBKC vuông tại K có
AD=BC
\(\widehat{ADH}=\widehat{BCK}\)
Do đó: ΔAHD=ΔBKC
Suy ra: HD=KC
Xét tứ giác ABKH có
AB//KH
AH=BK
Do đó: ABKH là hình bình hành
Suy ra: AB=HK
2: AB=HK=6cm
=>HD+KC=15-6=9(cm)
mà HD=KC
nên HD=CK=9/2=4,5(cm)