Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\text{#3107}\)
1.
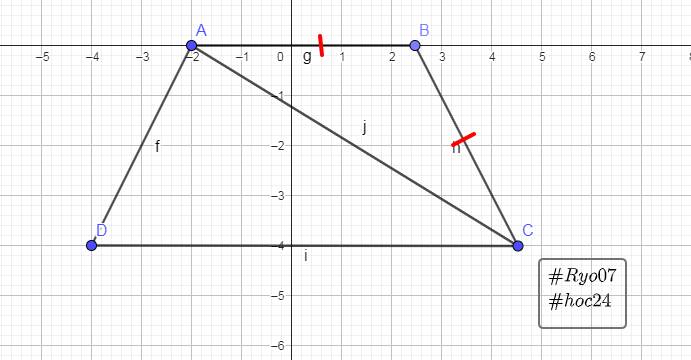
Ta có: \(\text{AB // CD}\)
\(\Rightarrow\widehat{\text{BAC}}=\widehat{\text{ACD}}\left(\text{2 góc sole trong}\right)\) `(1)`
Xét `\Delta ABC:`
\(\text{AB = BC (gt)}\)
\(\Rightarrow\) `\Delta ABC` cân tại B
\(\Rightarrow\widehat{\text{BAC}}=\widehat{\text{BCA}}\) `(2)`
Từ `(1)` và `(2)`
\(\Rightarrow\widehat{\text{ACB}}=\widehat{\text{ACD}}\)
Mà \(\widehat{\text{ACB}}+\widehat{\text{ACD}}=\widehat{\text{BCD}}\)
\(\Rightarrow\) CA là phân giác của \(\widehat{\text{BCD}}.\)

Bài 4:
Xét ΔAED vuông tại E và ΔBFC vuông tại F có
AD=BC
góc D=góc C
Do đó: ΔAED=ΔBFC
=>DE=CF
Bài 3:
a: Xét ΔADC và ΔBCD có
AD=BC
AC=BD
DC chung
Do đó: ΔADC=ΔBCD
=>góc ACD=góc BDC
b: Ta co: góc ACD=góc BDC
=>góc EAB=góc EBA
=>ΔEAB cân tại E
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{BCA}=\widehat{DCA}\)
hay CA là tia phân giác của \(\widehat{BCD}\)