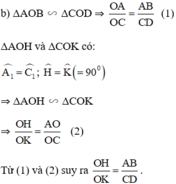Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

OA+OC=AC
OB+OD=BD
mà AC=BD và OC=OD
nên OA=OB
Xét ΔOAB vuông tại O có OA=OB
nên ΔOAB vuông cân tại O
=>góc OAB=góc OBA=45 độ
Xét ΔOCD vuông tại O có OC=OD
nên ΔOCD vuông cân tại O
=>góc OCD=góc ODC=45 độ
góc OAB=góc OCD=45 độ
mà hai góc này ở vị trí so le trong
nên AB//CD
Xét tứ giác ABCD có
AB//CD
AC=BD
=>ABCD là hình thang cân

Vì OE = AE và OF = DF => EF là đường TB của tam giác OAD => EF = AD/2 (1)
Vì ABCD là hình thang => góc OAB = OCD = 60* và ODC = OBA = 60*
==> tam giác OCD đều
∆ OCD đều có CF là đường trung tuyến nên đồng thời là đường cao => CF _l_ BD
=> tam giác BCF vuông tại F có trung tuyến FG => FG = BC / 2 (2)
Tương tự ==> EG = BC / 2 (3)
Vì 2 tam giác OAB và OCD đều => OA = OB và OC = OD
=> OA + OC = OB + OD <=> AC = BD => ABCD là hình thang cân => AD = BC (4)
Từ (1)(2)(3)(4) => EF = EG = FG => tam giác EFG đều
mọi người giúp mình với!!! mình cảm ơn nhiều
cho hình thang cân ABCD có góc ACD=60 độ. O là giao điểm của 2 đường chéo. gọi E,F,G theo thứ tự là trung điểm của OA,OD,BC. tam giác EFG là tam giác gì? tại sao?

a: Xét ΔACD và ΔBDC có
AC=BD
CD chung
AD=BC
Do đó: ΔACD=ΔBDC
Suy ra: ˆACD=ˆBDCACD^=BDC^
hay ˆODC=ˆOCDODC^=OCD^
Xét ΔOCD có ˆODC=ˆOCDODC^=OCD^
nên ΔOCD cân tại O
Suy ra: OC=OD
Ta có: AO+OC=AC
OB+OD=BD
mà AC=BD
và OC=OD
nên OA=OB

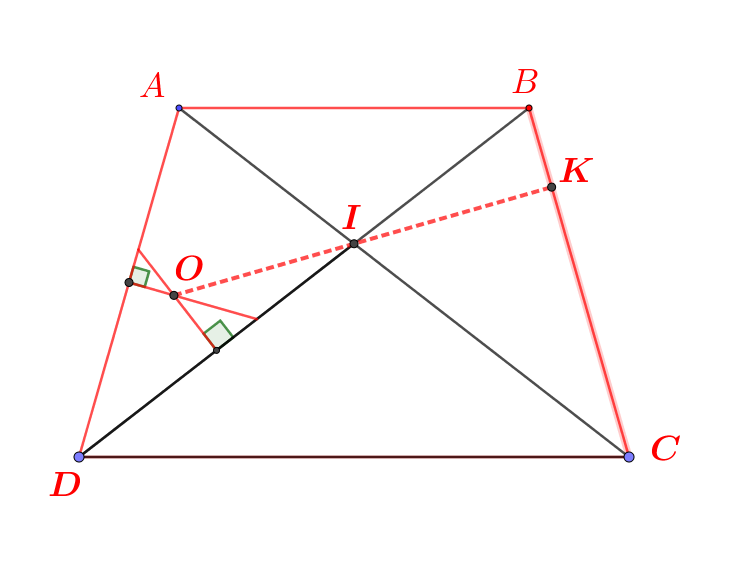
Cho tứ giác ABCD có 2 đường chéo AC và BD bằng nhau và cắt nhau tại O sao cho OC > OD. Gọi F, E, P, Q theo thứ tự là trung điểm AB, BC, CD, AD. Gọi Ot là phân giác góc DOC. Chứng minh rằng: Ot vuông góc QE.
Các bạn giúp mình với.. Mình sắp nộp bài rồi. Giải cụ thể nhé. Camon.
Vì OE = AE và OF = DF => EF là đường TB của tam giác OAD => EF = AD/2 (1)
Vì ABCD là hình thang => góc OAB = OCD = 60* và ODC = OBA = 60*
==> tam giác OCD đều
∆ OCD đều có CF là đường trung tuyến nên đồng thời là đường cao => CF _l_ BD
=> tam giác BCF vuông tại F có trung tuyến FG => FG = BC / 2 (2)
Tương tự ==> EG = BC / 2 (3)
Vì 2 tam giác OAB và OCD đều => OA = OB và OC = OD
=> OA + OC = OB + OD <=> AC = BD => ABCD là hình thang cân => AD = BC (4)
Từ (1)(2)(3)(4) => EF = EG = FG => tam giác EFG đều
Vì OE = AE và OF = DF => EF là đường TB của tam giác OAD => EF = AD/2 (1)
Vì ABCD là hình thang => góc OAB = OCD = 60* và ODC = OBA = 60*
==> tam giác OCD đều
∆ OCD đều có CF là đường trung tuyến nên đồng thời là đường cao => CF _l_ BD
=> tam giác BCF vuông tại F có trung tuyến FG => FG = BC / 2 (2)
Tương tự ==> EG = BC / 2 (3)
Vì 2 tam giác OAB và OCD đều => OA = OB và OC = OD
=> OA + OC = OB + OD <=> AC = BD => ABCD là hình thang cân => AD = BC (4)
Từ (1)(2)(3)(4) => EF = EG = FG => tam giác EFG đều

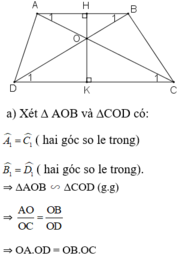
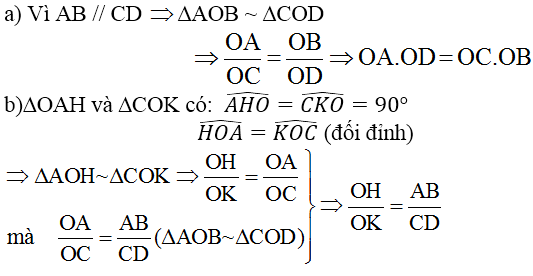
a;Vì AB//CD nên theo định lí Ta-lét ta có:
\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
\(\Rightarrow OA.OD=OC.OB\)
b;Xét \(\Delta AOH\) và \(\Delta COK\)có:
\(\widehat{AHO}=\widehat{CKO=90^o}\)
\(\widehat{AOH}=\widehat{COK}\) (hai góc đối đỉnh)
\(\Rightarrow\Delta AOH~\Delta COK\left(g.g\right)\)
\(\Rightarrow\dfrac{OA}{OC}=\dfrac{OH}{OK}\left(1\right)\)
Vì AB//CD nên theo hệ quả của định lí Ta-lét ta có
\(\dfrac{AB}{CD}=\dfrac{OA}{OC}\left(2\right)\)
Từ 1 và 2 ta có:
\(\dfrac{OH}{OK}=\dfrac{AB}{CD}\)