Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Ta có: AB//CD
=>\(\hat{OAB}=\hat{ODC}\) (hai góc đồng vị) và \(\hat{OBA}=\hat{OCD}\) (hai góc đồng vị)
mà \(\hat{ODC}=\hat{OCD}\)
nên \(\hat{OAB}=\hat{OBA}\)
=>ΔOAB cân tại O
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ΔABD=ΔBAC
=>\(\hat{ABD}=\hat{BAC}\)
=>\(\hat{EAB}=\hat{EBA}\)
=>EA=EB
Ta có: EA+EC=AC
EB+ED=BD
mà EA=EB và AC=BD
nên EC=ED
d: Ta có: OA+AD=OD
OB+BC=OC
mà AO=OB và AD=BC
nên OD=OC
=>O nằm trên đường trung trực của DC(1)
Ta có: EC=ED
=>E nằm trên đường trung trực của CD(2)
Từ (1),(2) suy ra OE là đường trung trực của CD
=>OE đi qua trung điểm của CD
=>O,E,trung điểm của CD thẳng hàng

Sửa đề: ABCD là hình thang cân
a: AB//CD
=>\(\hat{OAB}=\hat{ADC}\) (hai góc đồng vị) và \(\hat{OBA}=\hat{BCD}\) (hai góc đồng vị)
mà \(\hat{ADC}=\hat{BCD}\) (ABCD là hinh thang cân)
nên \(\hat{OAB}=\hat{OBA}\)
=>ΔOAB cân tại O
b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔBAD=ΔABC

- Bài 1
a) Xét tam giác BCD có BM=MD(gt), BN=NC(gt) => MN là đg` TB => MN// DC => MN// DE(1)
và MN=1/2DC => MN= DE(2)
từ (1)và (2) => MNED là hbh
b) MNED là hbh(câu a) => MD//NE => ADM= DEN(đồng vị)
Xét tam giác ABD vg tại A có BM=DM=> AM là trung tuyến => AM=1/2BD= MD
=> tam giác ADM cân tại M => MDA = DAM
=> DEN= MAD (3)
MN//DE=> MN//AE => AMNE là hình thang (4)
từ (3)và (4) => AMNE là hình thang cân
c) để MNED là hình thoi \Leftrightarrow MNED là hbh có MD=DE \Leftrightarrow 1/2BD=1/2CD \Leftrightarrow BD = CD \Leftrightarrow tam giác BCD cân tại D \Leftrightarrow DBC=góc C \Leftrightarrow góc C=1/2góc B\Leftrightarrow góc C=2góc B
Vậy để MNED là hình thoi thì tam giác ABC có góc C=2góc B17 Tháng mười hai 2013#2 
nhuquynhdatGuest
bài 2
a) AB//CD => AB//CE(1)
Xét tam giác ADE có AH là đg` cao
lại có E đối xứng với D qua H => H là trung điểm của DE => AH là trung tuyến
=> tam giác ADE cân tại A
=> ADE=AED(goác đáy tam giác cân)
mặt khác ABCD là hình thang cân => ADC=góc C
=> góc C= AED
mà 2 góc này ở vị trí đồng vị của AE và BC => AE//BC(2)
từ (1)và (2) => ABCE là hbh
b) xét tam giác AHE và tam giác FHD có góc AHE=góc DHF(đối đỉnh)
DH=HE(gt)
AE//DF(gt)=> AEH=FDH(SLT)
=>tam giác AHE=tam giác FHD(gcg) => AH=HF => H là TĐ của AF
c) Ta có AH=HF(câu b)DH=HE(gt) => ADFE là hbh
mà AH vg góc với ED=> AF vg góc với ED => ADEF là hình thoi
lại có tam giác ADE cân tại A (câu a)=> AD=AE => ADEF là hình vg

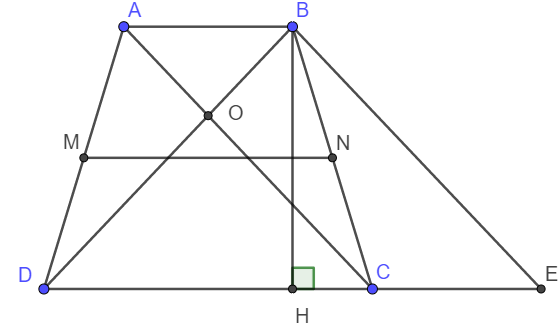
a) Xét tứ giác ABEC có AB // CE; AC // BE .
Vậy nên ABEC là hình bình hành. Suy ra AB = CE.
Do MN là đường trung bình hình thang ABCD nên ta có :
\(MN=\frac{AB+DC}{2}=\frac{CE+DC}{2}=\frac{DE}{2}.\)
b) Do ABCD là hình thang cân nên ta có:
\(AD=BC;DB=AC\)
Xét tam giác ABD và tam giác BAC có:
Cạnh AB chung
AD = BC
BD = AC
\(\Rightarrow\Delta ABD=\Delta BAC\left(c-c-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{BAC}\) hay \(\widehat{ABO}=\widehat{BAO}\)
Xét tam giác OAB có \(\widehat{ABO}=\widehat{BAO}\) nê OAB là tam giác cân tại O.
c) Do ABEC là hình bình hành nên AC = BE
Lại có AC = BD nên BD = BE
Suy ra tam giác BDE cân tại B.
Tam giác cân BDE có BH là đường cao nên đồng thời là đường trung tuyến.
Lại có theo câu a thì MN = DE/2
Giả thiết lại cho MN = BH. Vậy nên BH = DE/2
Xét tam giác BDE có trung tuyến BH bằng một nửa cạnh tướng ứng nên BDE là tam giác vuông tại B.
Vậy BDE là tam giác vuông cân tại B.

a: AB//CD
=>\(\hat{OAB}=\hat{ADC}\) (hai góc đồng vị) và \(\hat{OBA}=\hat{BCD}\) (hai góc đồng vị)
mà \(\hat{ADC}=\hat{BCD}\) (ABCD là hình thang cân)
nên \(\hat{OAB}=\hat{OBA}\)
=>ΔOAB cân tại O
b: Xét ΔABD và ΔBAC có
AB chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: Xét ΔADC và ΔBCD có
AD=BC
DC chung
AC=BD
Do đó: ΔADC=ΔBCD
=>\(\hat{ACD}=\hat{BDC}\)
=>\(\hat{EDC}=\hat{ECD}\)
=>ΔECD cân tại E
=>EC=ED

Chọn D