Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

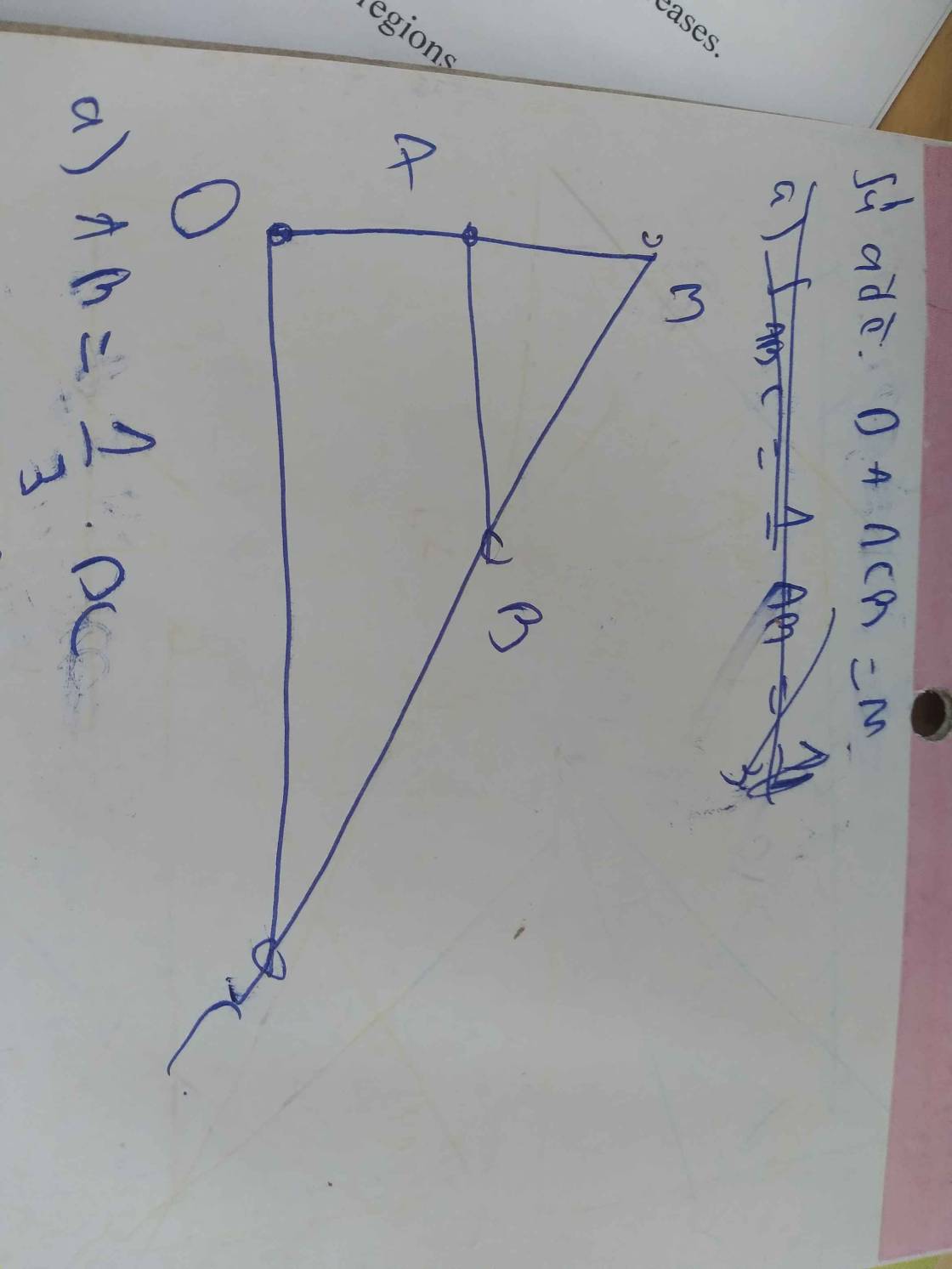
a: Xét ΔOBA và ΔODC có
góc OBA=góc ODC
góc BOA=góc DOC
=>ΔOBA đồng dạng với ΔODC
=>OB/OD=OA/OC=AB/CD=1/3
=>S ABO=1/3*S ABC
=>S BOC=2/3*S ABC
b: Kẻ CH vuông góc AB
=>S ABC=1/2*CH*AB
S ABCD=1/2*CH*(AB+CD)
=>S ABC/S ABCD=AB/(AB+CD)

a/ Xét 2 tam giác ABC và ABD có: Cạnh đáy AB chung
Đường cao hạ từ D và C xuống AB có độ dài bằng nhau (Vì AB//CD)
=> Diện tích của 2 tam giác bằng nhau (Vì có đáy và đường cao bằng nhau)
b/ Gọi h là đường cao của hình thang (cũng chính là chiều cao của tam giác BCD). Ta có:
\(S_{BCD}=\frac{1}{2}.DC.h=\frac{DC.h}{2}\)
Và: \(S_{ABCD}=\frac{\left(AB+CD\right).h}{2}=\frac{\left(\frac{2}{3}.DC+DC\right)}{2}=\frac{5DC.h}{6}\)
Tỉ số diện tích là: \(\frac{S_{BCD}}{S_{ABCD}}=\frac{DC.h}{2}:\frac{5DC.h}{6}=\frac{DC.h}{2}.\frac{6}{5DC.h}=\frac{3}{5}\)
=> Tỉ số % diện tích là: \(\frac{S_{BCD}}{S_{ABCD}}=\frac{3}{5}.100\%=60\%\)
Đáp số: 20%