Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có:
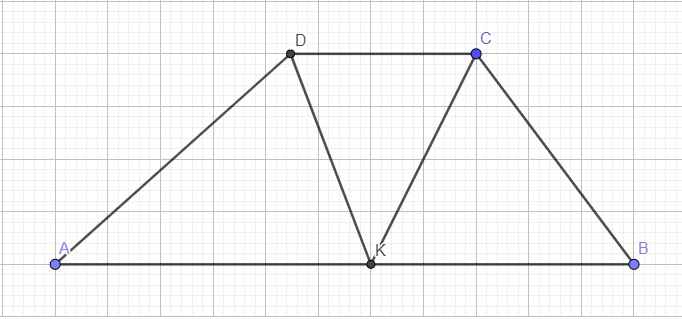
\(AB||CD\Rightarrow\widehat{AKD}=\widehat{CDK}\) (so le trong)
Mà \(\widehat{CDK}=\widehat{ADK}\) (do DK là phân giác góc D)
\(\Rightarrow\widehat{ADK}=\widehat{AKD}\)
\(\Rightarrow\Delta ADK\) cân tại A
\(\Rightarrow AD=AK\) (1)
Tương tự ta có: \(\widehat{DCK}=\widehat{BKC}\) (so le trong)
\(\widehat{DCK}=\widehat{BCK}\) (CK là phân giác góc C)
\(\Rightarrow\widehat{BCK}=\widehat{BKC}\Rightarrow\Delta BCK\) cân tại B
\(\Rightarrow BC=BK\) (2)
(1);(2) \(\Rightarrow AB=AK+BK=AD+BC\) (đpcm)

a) Gọi M và N lần lượt là giao điểm của AE, BF với CD.
Ta có: A D E ^ = 1 2 D ^ ngoài, D A E ^ = 1 2 A ^ ngoài.
Mà A ^ ngoài + D ^ ngoài = 1800 (do AB//CD)
⇒ A D E ^ + D A E ^ = 90 0 , tức là tam giác ADE vuông tại E.
Khi đó, tam giác ADM cân tại D (do có DE vừa là đường phân giác, vừa là đường cao) và E là trung điểm của AM.
Chứng minh tương tự, ta được F olaf trung điểm của BN.
Từ khó, suy ra EF là đường trung bình của hình thang ABNM và ta được ĐPCM
b) Từ ý a), EF = 1 2 ( A B + B C + C D + D A )