Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2. A B C D O E F
+ AB // CD \(\Rightarrow\dfrac{AO}{CO}=\dfrac{BO}{DO}\)
\(\Rightarrow\dfrac{AO}{AO+CO}=\dfrac{BO}{BO+DO}\Rightarrow\dfrac{AO}{AC}=\dfrac{BO}{BD}\)
+ OE // CD => \(\dfrac{OE}{CD}=\dfrac{AO}{AC}\)
+ OF // CD => \(\dfrac{OF}{DC}=\dfrac{BO}{BD}\)
\(\Rightarrow\dfrac{OE}{CD}=\dfrac{OF}{DC}\Rightarrow OE=OF\)
Bài 1:
a: Xét hình thang ABCD có MN//AB//CD
nên AM/MD=BN/NC
b: AM/MD=BN/NC
=>MD/AM=NC/BN
=>\(\dfrac{MD+AM}{AM}=\dfrac{NC+BN}{BN}\)
=>AD/AM=BC/BN
=>AM/AD=BN/BC
c: AM/AD=BN/BC
=>1-AM/AD=1-BN/BC
=>DM/AD=CN/CB

a: Xét ΔOAB và ΔOCD có
\(\widehat{OAB}=\widehat{OCD}\)
\(\widehat{AOB}=\widehat{COD}\)
Do đó; ΔOAB\(\sim\)ΔOCD
Suy ra: OA/OC=OB/OD
hay \(OA\cdot OD=OB\cdot OC\)
b: Ta có; ΔOAB\(\sim\)ΔOCD
nên AB/CD=OB/OD=OA/OC
=>5/CD=OB/3,6=2/4=1/2
=>CD=10cm; OB=1,8(cm)

A B C O D E F
a
Ta có:
\(OA=AD-OD=\frac{2S_{ABC}}{BC}-\frac{2S_{BOC}}{BC}=\frac{2\left(S_{ABC}-S_{BOC}\right)}{BC}\)
\(OD=2S_{BOC}\Rightarrow\frac{OA}{OD}=\frac{S_{ABC}-S_{BOC}}{S_{BOC}}=\frac{S_{ABC}}{S_{BOC}}-1\Rightarrow\frac{OA}{OD}+1=\frac{S_{ABC}}{S_{BOC}}\)
Tương tự
\(\frac{OB}{OE}+1=\frac{S_{ABC}}{S_{COA}};\frac{OC}{OD}+1=\frac{S_{ABC}}{S_{AOB}}\)
Cộng vế theo vế ta có:
\(\frac{OA}{OD}+\frac{OB}{OE}+\frac{OC}{OF}+3=S_{ABC}\left(\frac{1}{S_{AOB}+S_{BOC}+S_{COA}}\right)\left(1\right)\)
Áp dụng BĐT s-vác ta có:
\(\frac{OA}{OD}+\frac{OB}{OE}+\frac{OC}{OF}+3\ge S_{ABC}\cdot\frac{9}{S_{AOB}+S_{BOC}+S_{COA}}=\frac{9S_{ABC}}{S_{ABC}}=9\)
\(\Rightarrowđpcm\)
Dấu "=" xảy ra tại \(S_{OAB}=S_{OBC}=S_{COA}\Leftrightarrow O\) là trọng tâm của tam giác.
b
Em nghĩ đề là \(\frac{OA}{OD}\cdot\frac{OB}{OE}\cdot\frac{OC}{OF}\ge8\)
Nếu vậy thì e lm như sau:
Ta có:\(\frac{OA}{OD}=\frac{S_{ABC}-S_{BOC}}{S_{BOC}}=\frac{S_{AOC}+S_{AOB}}{S_{BOC}}\)
Tương tự ta có:\(\frac{OB}{OE}=\frac{S_{BOA}+S_{BOC}}{S_{COA}};\frac{OC}{OF}=\frac{S_{COA}+S_{COB}}{S_{BOA}}\)
Đặt \(\left(S_{COA};S_{BOA};S_{BOC}\right)\rightarrow\left(S_1;S_2;S_3\right)\)
Ta có:
\(\frac{OA}{OD}\cdot\frac{OB}{OE}\cdot\frac{OC}{OF}=\frac{\left(S_1+S_2\right)\left(S_2+S_3\right)\left(S_3+S_1\right)}{S_1\cdot S_2\cdot S_3}\)
Áp dụng BĐT Cô si ta có:
\(S_1+S_2\ge2\sqrt{S_1\cdot S_2};S_2+S_3\ge2\sqrt{S_2\cdot S_3};S_3+S_1\ge2\sqrt{S_3\cdot S_1}\)
\(\Rightarrow\frac{OA}{OD}\cdot\frac{OB}{OE}\cdot\frac{OC}{OF}\ge\frac{8\cdot S_1\cdot S_2\cdot S_3}{S_1\cdot S_2\cdot S_3}=8\)
Dấu "=" xảy ra tại \(S_1=S_2=S_3\Leftrightarrow O\) là trọng tâm tam giác ABC.
Câu a. Dòng đầu tiên là nhầm rồi Huy. AD đâu phải đường cao đâu thế tại sao: \(AD=\frac{2S_{\Delta ABC}}{BC}\)???
Bài này có thể giải:
a.
Có: \(\frac{OA}{OD}=\frac{AD-OD}{OD}=\frac{AD}{OD}-1=\frac{S_{\Delta ABC}}{S_{\Delta OBC}}-1\)
Tương tự: \(\frac{OB}{OE}=\frac{S_{BAC}}{S_{OAC}}-1\); \(\frac{OC}{OF}=\frac{S_{CAB}}{S_{OAB}}-1\)
=> \(\frac{OA}{OD}+\frac{OB}{OE}+\frac{OC}{OF}=\frac{S_{ABC}}{S_{OBC}}+\frac{S_{ABC}}{S_{OAC}}+\frac{S_{ABC}}{S_{OAB}}-3\)
\(=S_{ABC}\left(\frac{1}{S_{OBC}}+\frac{1}{S_{OAC}}+\frac{1}{S_{OAB}}\right)-3\ge S_{ABC}.\frac{\left(1+1+1\right)^2}{S_{OBC}+S_{OAC}+S_{OAB}}-3=\frac{S_{ABC}.9}{S_{ABC}}-3=6\)
"=" xảy ra <=> O là trọng tâm
b. Làm đúng rồi.

Giải:
a) Nối AC cắt EF tại O
∆ADC có EO // DC => AEEDAEED = AOOCAOOC (1)
∆ABC có OF // AB => AOOCAOOC = BFFCBFFC (2)
Từ 1 và 2 => AEEDAEED = BFFCBFFC
b) Từ AEEDAEED = BFFCBFFC => AEED+AEAEED+AE= BFFC+BFBFFC+BF

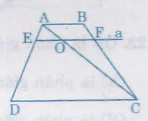
a) AB//CD => góc BAC = góc DCA ( so le trong)
Xét tam giác ABO và tam giác CDO có:
góc BAC = góc DCA (cmt)
góc AOB = góc COD (đối đỉnh)
=> tam giác ABO ~ tam giác CDO (TH3)
=> \(\dfrac{OA}{OB}\) = \(\dfrac{OC}{OD}\)
=> OA. OD = Oc. OB (đpcm)
b) Xét tam giác HOA và tam giác KOC có:
góc HOA = góc KOC (đối đỉnh)
góc BAC = góc DCA (cmt)
=> tam giác HOA ~ tam giác KOC (TH3)
c) Ta có:
+) AB//CD => \(\dfrac{AB}{CD}\) = \(\dfrac{OA}{OC}\)(hệ quả định lí Talet)(1)
+) AB//CD ; H \(\in\) AB; K \(\in\) DC => AH//KC
=> \(\dfrac{OH}{OK}\) = \(\dfrac{OA}{OC}\)( hệ quả định lí Talet)(2)
Từ (1) và (2) => \(\dfrac{AB}{CD}\) =\(\dfrac{OH}{OK}\) (đpcm)
![]()

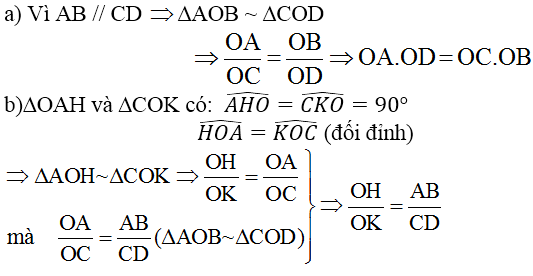
a;Vì AB//CD nên theo định lí Ta-lét ta có:
\(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
\(\Rightarrow OA.OD=OC.OB\)
b;Xét \(\Delta AOH\) và \(\Delta COK\)có:
\(\widehat{AHO}=\widehat{CKO=90^o}\)
\(\widehat{AOH}=\widehat{COK}\) (hai góc đối đỉnh)
\(\Rightarrow\Delta AOH~\Delta COK\left(g.g\right)\)
\(\Rightarrow\dfrac{OA}{OC}=\dfrac{OH}{OK}\left(1\right)\)
Vì AB//CD nên theo hệ quả của định lí Ta-lét ta có
\(\dfrac{AB}{CD}=\dfrac{OA}{OC}\left(2\right)\)
Từ 1 và 2 ta có:
\(\dfrac{OH}{OK}=\dfrac{AB}{CD}\)
Xét hình thang ABCD có EF//AB//CD
nên AE/AD=BF/BC(1)
Xét ΔADC có EO//DC
nên EO/DC=AE/AD(2)
Xét ΔBDC có OF//DC
nên OF/DC=BF/BC(3)
Từ (1), (2) và (3) suy ra OE=OF