Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A

Tam giác ABC đều có R Δ A B C = 2 a 3 3 ⇒ A B = 2 a .
Dựng hình lăng trụ ABCD.A’B’C’D’, O là trung điểm của B’D’
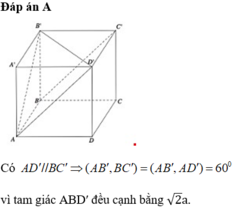
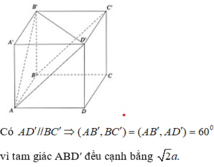
khi đó B C ' / / A D ' ⇒ B ' A D ' ^ = 60 ∘ ⇒ Δ A B ' D đều cạnh
B ' D ' = 2 a 3 ⇒ A D = 2 a 3 ⇒ A A ' = A ' D 2 − A D 2 = 2 a 2
Lại có:
d A B ' ; B C ' = d B C ' ; A B ' D ' = d B ; A B ' D ' = d A ' ; A ' B ' D ' = A ' H = A ' O . AA' A ' O 2 + A A ' 2 = 2 a 2 3 .

Đáp án A
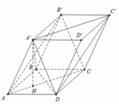
Do các góc phẳng đỉnh A đều bằng 60 ∘ và
nên các tam giác A ’ A D ; A ’ A B ; A B D là các tam giác đều cạnh 1.
Ta có:
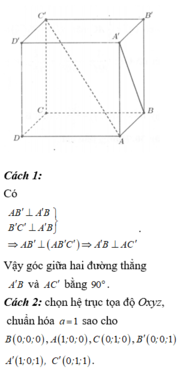
A ' C ' / / A C ⇒ d A B ' ; A ' C ' = d A B ' C ; A ' C ' = d C ' ; A B ' C = 3 V C ' . A B ' C S . A B ' C
Mặt khác A ’ . A B D là hình tứ diện đều cạnh 1.
Ta có A H = 2 3 . A O = 3 3 ⇒ A ' H = A A ' 2 − A H 2 = 6 3 .
V = S A B C D = V A . C C ' B ' = 1 2 V A . C C ' B ' B = V 6 = 2 12
Δ A B ' C ' cân tại A có A B ' = A C = 3 ; B ' C = A ' D = 1
S A B ' C = 11 4 ⇒ d = 3. 2 12 11 4 = 22 11 .

Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ ( B B ' D ' D ) ⇒ B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)
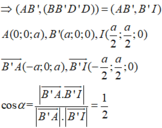

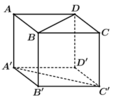
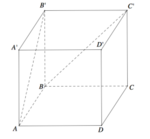
Ta có khoảng cách giữa hai đường thẳng chéo nhau BD và A'C' bằng khoảng cách giữa mặt phẳng song song (ABCD) và (A'B'C'D') thứ tự chứa BD và A'C' (hình vẽ). Do đó khoảng cách giữa hai đường thẳng BD và A'C' bằng a Chọn A.
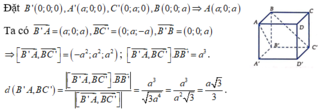


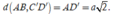
Gọi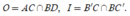
Suy ra OI//AB'. Khi đó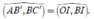
Ta có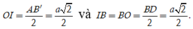
Suy ra
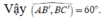
Chọn C.