Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
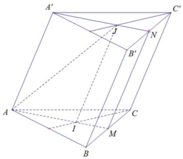
Xét tam giác A’B’C’:
Gọi N là trung điểm B’C’
J là trọng tâm A’B’C’
![]()
Xét tam giác ABC:
Gọi M là trung điểm BC
I là trọng tâm ABC
![]()
Từ (1), (2), ta có IJ // MN
Xét (AIJ) và (B’C’CB) có:
M là điểm chung
IJ // MN
⇒ giao tuyến của (AIJ) và (B’C’CB) là MN
⇒ thiết diện cần tìm là mặt phẳng (A’NMA)
Xét (A’NMA) có: A’A // MN và A’A = MN ( // = BB’)
A’NMA là hình hình hành

Đáp án D
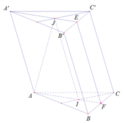
Gọi E và F lần lượt là trung điểm của B’C’ và BC
Xét (AIJ) và (ABC) có: F ∈ AI ⇒ F ∈ (AIJ) ⇒ (AIJ) ∩ (ABC) = AF
Xét ( AIJ) và (B’C’CB) có : F là điểm chung
IJ // (B’C’CB) ( I; J lần lượt là trọng tâm tam giác ABC và A’B’C’)
⇒ giao tuyến của 2 mặt phẳng là đường thẳng a đi qua F và song song IJ
a cắt B’C’ tại E
⇒ (AIJ) ∩ (B’C’CB) = EF
Xét ( AIJ) và (A’B’C’) có:
E là điểm chung
AF // (A’B’C’)
⇒ giao tuyến 2 mặt phẳng là đường thẳng b đi qua E và song song AF
⇒ (AIJ) ∩ (A’B’C’) = A’E
Xét A’EFA có: AA’ // EF ( // IJ)
A’E // AF
A’EFA là hình bình hành

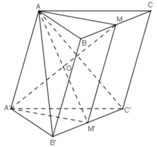
a) Do ABC.A’B’C’ là hình lăng trụ nên ta có: BCC’B’ là hình bình hành
Xét tứ giác BCC’B’ có M và M’ lần lượt là trung điểm của BC và B’C’ nên MM’ là đường trung bình
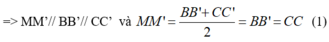
Lại có: AA’// BB’ và AA’= BB’ ( tính chất hình lăng trụ) (2)
Từ (1) và (2) suy ra: MM’// AA’ và MM’ = AA’
=> Tứ giác AMM’A’ là hình bình hành
b) Trong (AMM’A’) gọi O = A’M ∩ AM’, ta có :
Ta có : O ∈ AM’ ⊂ (AB’C’)
⇒ O = A’M ∩ (AB’C’).
c)
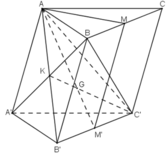
Gọi K = AB’ ∩ BA’, ta có :
K ∈ AB’ ⊂ (AB’C’)
K ∈ BA’ ⊂ (BA’C’)
⇒ K ∈ (AB’C’) ∩ (BA’C’)
Dễ dàng nhận thấy C’ ∈ (AB’C’) ∩ (BA’C’)
⇒ (AB’C’) ∩ (BA’C’) = KC’.
Vậy d cần tìm là đường thẳng KC’
d) Trong mp(AB’C’), gọi C’K ∩ AM’ = G.
Ta có: G ∈ AM’ ⊂ (AM’M)
G ∈ C’K.
⇒ G = (AM’M) ∩ C’K.
+ K = AB’ ∩ A’B là hai đường chéo của hình bình hành ABB’A’
⇒ K là trung điểm AB’.
ΔAB’C’ có G là giao điểm của 2 trung tuyến AM’ và C’K
⇒ G là trọng tâm ΔAB’C’.

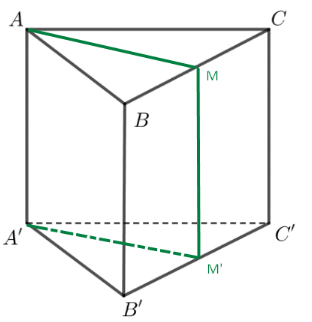
Ta có M, M' lần lượt là trung điểm của BC, B'C', BCC'B' là hình bình hành suy ra MM' // CC'.
Vì các cạnh bên của hình lăng trụ ABC.A'B'C' đôi một song song nên AA'//CC'.
Mặt phẳng ((AMC) //(A'M'C') nên AMC. AM'C' là hình lăng trụ.

Chọn D
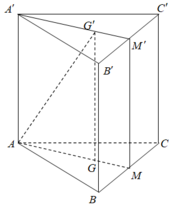
Gọi M, M' lần lượt là trung điểm của BC và B’C’. Khi đó thiết diện của lăng trụ tạo bởi mặt phẳng (AGG') là hình chữ nhật AMM'A’.
Mà A M ’ = a . s i n 60 0 = a 3 2 ≠ A A ’
Nên AMM’A’ không thể là hình vuông.

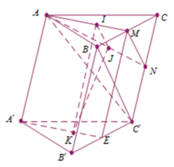
Gọi M, N, E lần lượt là trung điểm của BC, CC′, B′C′.
Suy ra (tính chất trọng tâm tam giác) nên IJ // MN (1).
Trong mặt phẳng (AA′ME) ta có
⇒ IK // ME
mà ME // BB′ nên IK // BB′ (2).
Từ (1) và (2) do (IJK) và (BB′C′) là hai mặt phẳng phân biệt
IJ; IK ∈ (IJK)
Nên IJ // (BB′C′), IK // (BB′C′)
Suy ra (IJK) // (BB′C′)
Đáp án cần chọn là: C

Ta có: ABB'A' là hình bình hành, M, N là trung điểm của AA', BB' nên MN // AB (đường trung bình) suy ra MN // (ABC).
Tương tự, ta có NP // BC suy ra NP// (ABC).
Mặt phẳng (MNP) chứa hai đường thẳng cắt nhau MN, NP và MN, NP song song với mp(ABC) suy ra (MNP) //(ABC).

B ' C → = A C → - A B ' → = A C → - ( A A ' → + A B → ) = c → - a → - b →
Đáp án B

A G → = A A ' → + A ' G → = A A ' → + 1 / 3 ( A ' B ' → + A ' C ' → ) = a → + 1 / 3 ( b → + c → )
Đáp án D
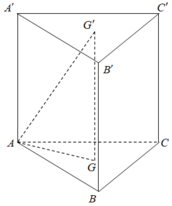
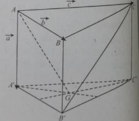
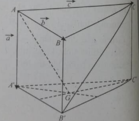
a) Ta có ABC.A'B'C' là hình lăng trụ nên \(\Delta ABC = \Delta A'B'C'\) suy ra AG = A'G'.
Lại có (ABC) // (A'B'C'), giao tuyến của mp(AGG'A') với (ABC) và (A'B'C') lần lượt là AG, A'G' suy ra AG // A'G'.
Như vậy , tứ giác AGG'A' có AG = A'G', AG // A'G' là hình bình hành.
b) AGG'A' là hình bình hành suy ta AA' // GG'.
Lại có AA' // CC' (do ABC.A'B'C' là hình lăng trụ).
Mặt phẳng (AGC) // (A'G'C') suy ra AGC.A'G'C' là hình lăng trụ.