Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Diện tích xung quanh lăng trụ là :
\(\left(10+2+2.5\right).5=110\left(m^2\right)\)
Diện tích toàn phần lăng trụ là :
\(110+2.\left(10+2\right).3.\dfrac{1}{2}=146\left(m^2\right)\)
Đáp số...

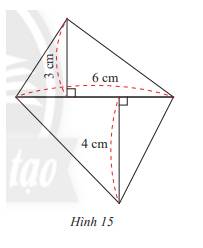
Diện tích đáy của lăng trụ là:
\(\dfrac{1}{2}.3.6+\dfrac{1}{2}.4.6\) = 21 (cm2)
Tính thể tích lăng trụ đứng là:
V = Sđáy . h = 21.7 = 147 (cm3)

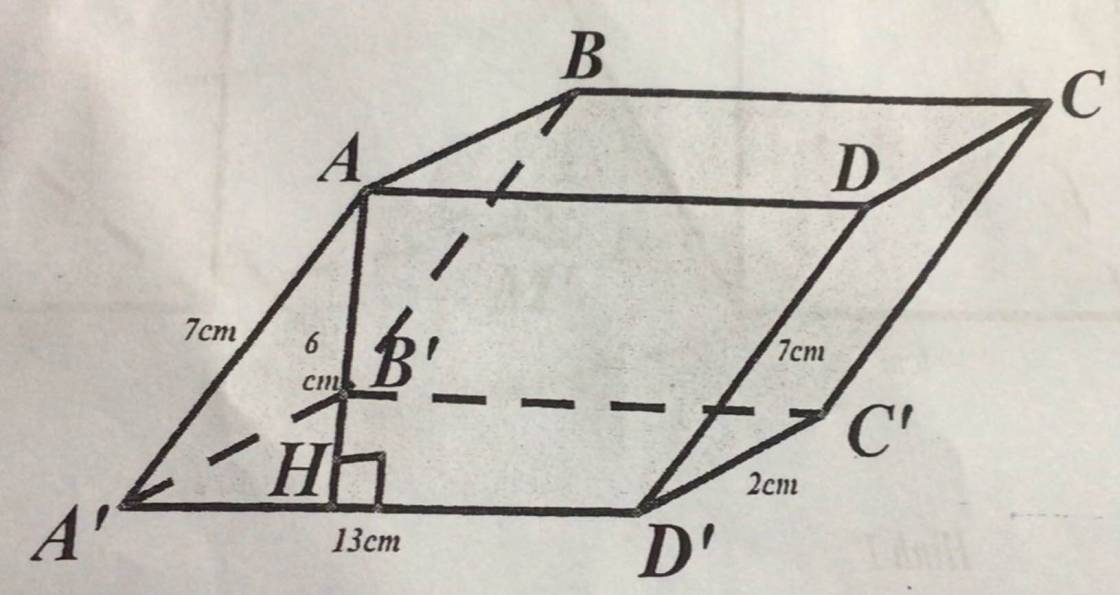
Ta có Sxq= chu vi đáy (hình bình hành) nhân chiều cao= 2.(7+13).2=80 cm vuông
Ta có V(thể tích)= S đáy . Chiều cao=6.13.2=156 cm khối
Chúc bạn học tốt và nhớ đọc kỹ kiến thức trong sách giáo khoa

Lời giải:
Chu vi đáy lăng trụ: $6+7+9=22$ (cm)
Diện tích xung quanh lăng trụ: $22.13=286$ (cm2)

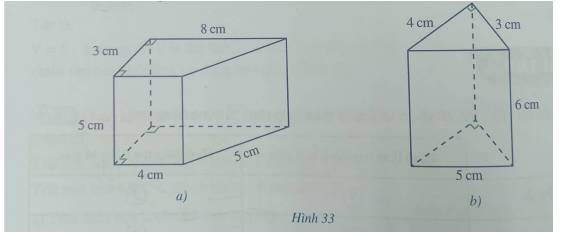
i) Hình 33b là hình lăng trụ đứng tam giác
Hình 33a là hình lăng trụ đứng tứ giác
ii) Hình 33a: Sxq = (3+4+5+8).5 = 100 (cm2)
Hình 33b: Sxq = (3+4+5).6 = 72 (cm2)
iii) Hình 33a: Diện tích đáy là: (8+4).3:2=18 (cm2)
Thể tích là: V = 18.5 = 90 (cm3)
Hình 33b: Diện tích đáy là: \(\dfrac{1}{2}3.4=6\) (cm2)
Thể tích là: V= 6.6=36 (cm3)

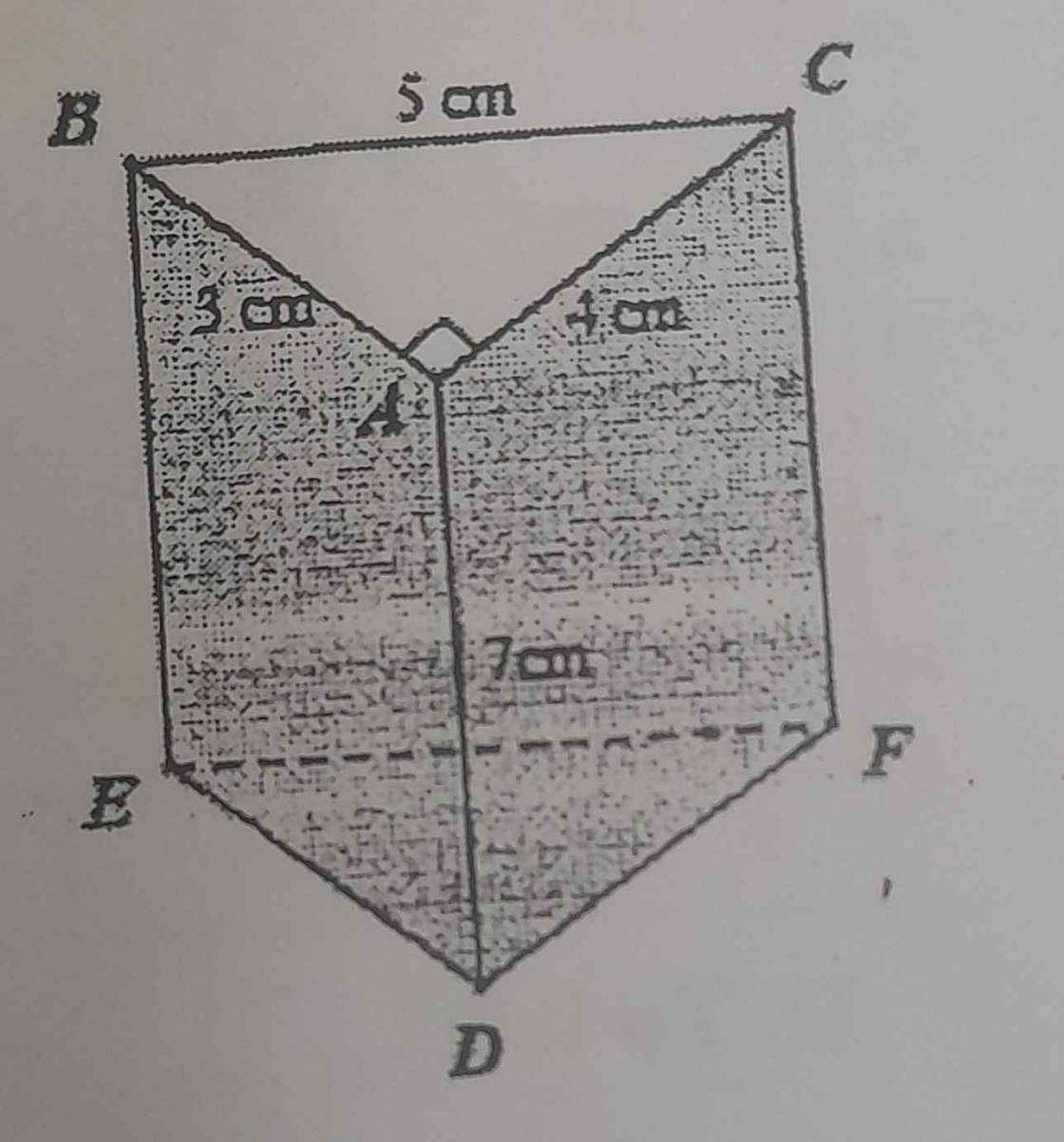
Chu vi đáy là 3+4+5=12(cm)
Diện tích xung quanh của hình trụ là:
\(S_{xq}=12\cdot7=84\left(cm^2\right)\)
Vì \(AB^2+AC^2=BC^2\)
nên ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)
Thể tích của lăng trụ là:
\(V=S_{đáy}\cdot cao=6\cdot7=42\left(cm^3\right)\)

Vì \(9^2+12^2=15^2\) nên ở đáy là tam giác vuông.
Diện tích mặt đáy là:
\(\dfrac{9\cdot12}{2}=54\left(m^2\right)\)
Chu vi mặt đáy là:
\(9+12+5=26\left(m\right)\)
Diện tích xung quanh lăng trụ:
\(26\cdot5=130\left(m^2\right)\)
Diện tích toàn phần lăng trụ:
\(130+54\cdot2=238\left(m^2\right)\)
Thể tích lăng trụ:
\(54\cdot5=270\left(m^3\right)\)
ko nhìn rõ