Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) áp dụng định lý Pytago ta có:
BC2 = AB2 + AC2
\(\Rightarrow\)BC2 = 62 + 82 = 100
\(\Rightarrow\)BC = \(\sqrt{100}\)= 10
\(\Delta\)ABC vuông tại A có AM là trung tuyến
\(\Rightarrow\)AM = \(\frac{BC}{2}\)= \(\frac{10}{2}\)= 5cm
b) AKMN là hình chữ nhật vì \(\widehat{AKM}\)= \(\widehat{KAN}\)= \(\widehat{ANM}\)= 900
c) KM \(\perp\)AB; AB \(\perp\)AC
\(\Rightarrow\)KM // AC
\(\Delta ABC\)có KM // AC; MB = MC
\(\Rightarrow\)KA = KB
\(\Rightarrow\)KM là đường trung bình của \(\Delta ABC\)
\(\Rightarrow\)KM = \(\frac{AC}{2}\)
CM tương tự ta có: NC =\(\frac{AC}{2}\)
suy ra KM = NC
mà KM // NC
nên KMNC là hình bình hành

x 6cm 4cm Theo định lý Py - ta - go :
x2 = 42 + 62
⇒ x2 = 16 + 36
⇒ x2 = 52
⇒ x = √52 (cm)
Vậy đáp án (B) là chính xác
Nhắc lại : Đáp án (B)

a) xét tg IAB vuông tại I và tg CBD vuông tại C
có: ^ABI = ^CDB ( AB//CD)
=> tg IAB ~ tg CBD (g-g)
b) xét tg ADI vuông tại I và tg BDA vuông tại A
có: ^D chung
=> tg ADI ~ tg BDA (g-g)
=> AD/DB = DI/DA (t/c)
=> AD2 = DB.DI
c) ta có: \(DB=\sqrt{8^2+6^2}=10\left(cm\right)\)
mà AD2 = DB.DI
=> 36 = 10.DI
=> DI = 3,6 (cm)
mà IB = DB - DI = 10 -3,6 = 6,4 (cm)
...
bn tự kẻ hình nha

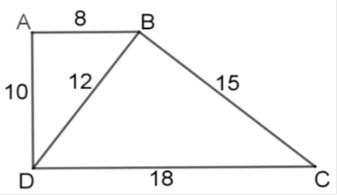
a) Xếp độ dài các cạnh của mỗi tam giác ABD và BDC từ nhỏ đến lớn:8,10,12 và 12,15,18.
Ta có \(\frac{8}{12}=\frac{10}{15}=\frac{12}{18}=\frac{2}{3}\)
=> ΔABC đồng dạng với ΔBDC ( theo c.c.c)
b) ΔABD đồng dạng với ΔBDC
nên \(\widehat{ABD}=\widehat{BDC}\) (So le trong)
=> AB//CD
=> ABCD là hình thang
chúc bạn học tốt:)

Bài giải:
Xét bài toán tổng quát:
ABCD là hình thoi, O là giao điểm hai đường chéo.
Theo định lí Pitago ta có:
AB2 = OA2 +OB2 = ( AC)2 + (
AC)2 + ( BD)2
BD)2
Suy ra AB = 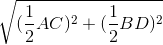
Do đó theo đề bài: AB = 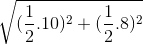
AB = 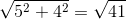
Vậy (B) đúng.
Xét bài toán tổng quát:
ABCD là hình thoi, O là giao điểm hai đường chéo.
Theo định lí Pitago ta có:
AB2 = OA2 +OB2 = ( AC)2 + (
AC)2 + ( BD)2
BD)2
Suy ra AB = 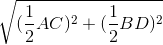
Do đó theo đề bài: AB = 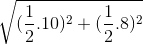
AB = 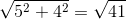
Vậy (B) đúng.
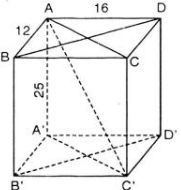


Vì ABCD.A’B’C’D’ là hình hộp chữ nhật nên tứ giác ABCD ; DCC’D’ và CBB’C’ là hình chữ nhật
Suy ra: BC = AD = 6cm; CC’ = DD’ = 8cm
Áp dụng đinh lí Py ta go vào tam giác BCC’ ta có:
B C ’ 2 = B C 2 + C C ’ 2 = 6 2 + 8 2 = 100
Suy ra: BC’ = 10cm
Chọn đáp án A