

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Hướng dẫn giải:
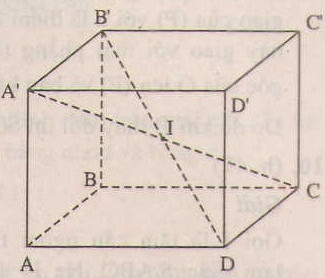
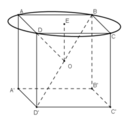
a) Trong hình hộp chữ nhật, bốn đường chéo AC", BD', CA" và DB" căt nhau tại điểm I là trung điểm của mỗi đường.
Vì 4 đường chéo trong hình hộp chữ nhật bằng nhau, nên điểm I cách đề 8 đỉnh của hình hộp chữ nhật. Nó là tâm của mặt cầu ngoại tiếp hình hộp.
Vì AB = b, AD = c, AA' = a nên bán kính mặt cầu 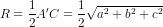 .
.
b) Giao tuyến của mặt phẳng ABCD với mặt cầu ngoại tiếp hình hộp chữ nhật ABCD.A'B'C'D' là hai đwòng tròn ngoại tiếp hình chữ nhật ABCD. Nên bán kính của đường trong giao tuyến là
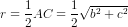

Chọn A.
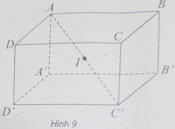
(h.9) Tâm của hình hộp chữ nhật cách đều 8 đỉnh của hình hộp nên tâm của mặt cầu (S) chính là tâm của hình hộp chữ nhật.

Chọn D.
Tâm của hình hộp chữ nhật cách đều 8 đỉnh của hình hộp nên tâm của mặt cầu (S) chính là tâm của hình hộp chữ nhật.
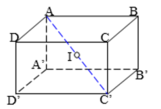

Tâm mặt cầu ngoại tiếp hình hộp chính là tâm đối xứng của hình hộp, tâm đối xứng của hình hộp là trung điểm AC'
\(r=\frac{\sqrt{a^2+b^2+c^2}}{2}\)

Đáp án B
Ta có: A C = A B 2 + B C 2 = a 5
Bán kính mặt cầu ngoại tiếp là 3 a 2 ⇒ A C ' = 3 a
Xét tam giác A C C ' vuông tại C, ta có: C C ' = A C ' 2 - A C 2 = 2 a
Thể tích hình hộp là:
V = C C ' . S A B C D = 2 a . a . 2 a = 4 a 3

Tâm là giao điểm các đường chéo (O)
Bán kính mặt cầu là OA = 1/2 AC’
Đường chéo hình vuông cạnh a là a√2 (AC = a√2)
Xét tam giác vuông ACC’ tại C:
⇒ bán kính mặt cầu đi qua 8 đỉnh hình lập phương là (a√3)/2