Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
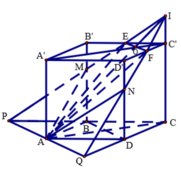
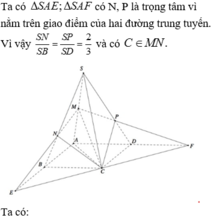
Dựng thiết diện: PQ qua A và song song với BD ( vì EF//B’D’//BD )
PE cắt các cạnh BB’, CC’ tại M và I. Tương tự ta tìm được giao điểm N. T iết diện là AMEFN.
Dựa vào đường trung bình BD và định lí Ta-lét cho các tam giác IAC, DNQ, D’NF ta tính được: I C ' = a 3 , N D = 2 a 3 Tương tự ta tính được: M B = 2 a 3
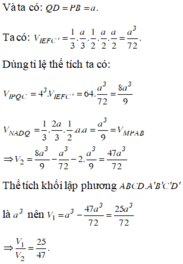

Đáp án A.
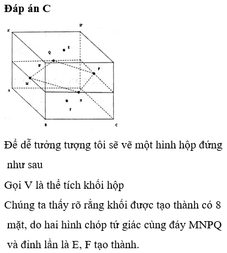
Đường thẳng EF cắt A'D' và A'B' tại N;M;AN cắt DD' tại P;AM cắt BB' tại Q. Khi đó thiết diện của hình lập phương khi cắt bởi mặt phẳng (AEF) là ngũ giác APFEQ
Từ giả thiết ta có V 1 = V A ' B ' D ' A P F E Q và V 2 = V A B C D C ' P F E Q ' .
Gọi
V = V A B C D . A ' B ' C ' D ' ; V 3 = V A . A ' M N ; V 4 = V P F D ' N ; V 5 = V Q M B ' E .
Do tính đối xứng của hình lập phương nên V 4 = V 5 .
Nhận thấy
V 3 = 1 6 A A ' . A ' M . A ' N = 1 6 . a . 3 a 2 . 3 a 2 = 3 a 2 8 (đvtt).
V 4 = 1 6 . D ' P . D ' F . D ' N = 1 6 . a 3 . a 2 . a 2 = a 3 72 (đvtt);
V 1 = V 3 − 2 V 4 = 3 a 3 8 − 2. a 3 72 = 25 a 3 72 (đvtt).
V 2 = V − V 1 = a 3 − 25 a 3 72 = 47 a 3 72 (đvtt).
Vậy V 1 V 2 = 25 47 .

Đáp án A
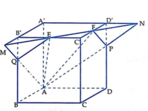
Ta chứng minh được công thức tỷ số thể tích tối với khối hộp như sau (học sinh có thể tự chứng minh).
V A ' B ' C ' D ' . M N P Q V A " B ' C ' D ' . A B C D = 1 2 A ' M A ' A + C ' P C ' C = 1 2 B ' N B ' B + D Q D ' D
Khi đó: 1 3 + 1 2 = 2 3 + D Q D ' D ⇔ D Q D ' D = 1 6 .

Đáp án D
Phương pháp: Sử dụng phương pháp tọa độ hóa.
Cách giải:
Gắn hệ trục Oxyz, có các tia Ox, Oy, Oz lần lượt trùng với các tia AB, AD, AA’.
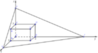
A(0;0;0), B(1;0;0), C(1;2;0), D(0;2;0), A’(0;0;3), B’(1;0;3), C’(1;2;3), D’(0;2;3)
(P) cắt các tia AB, AD, AA’ lần lượt tại E, F, G (khác A). Gọi E(a;0;0), F(0;b;0), G(0;0;c), (a,b,c > 0)
Phương trình mặt phẳng (P): x a + y b + c z = 1
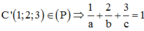
Thể tích tứ diện AEFG: 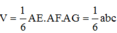
Ta có: 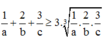

![]()
=>Vmin = 27 khi và chỉ khi 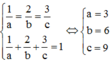
Khi đó, T = AE + AF + AG = a + b + c = 3 + 6 + 9 = 18

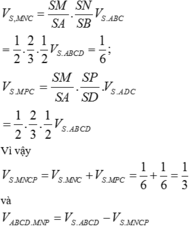


Đáp án C.
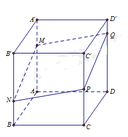
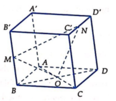
+ Trong mặt phẳng (BB’D’D) gọi I = M O ∩ DD ' , H = M O ∩ B ' D '
Trong mặt phẳng (DD’C’C) gọi J = N I ∩ D C
Trong mặt phẳng (ABCD) gọi K = J O ∩ A B
Trong mặt phẳng (AA’B’B) gọi F = M K ∩ A ' B '
Trong mặt phẳng (A’B’C’D’) gọi
E = B ' C ' ∩ F N ⇒ E = B C ∩ ( M N O )
BO = B’H = OD ⇒ C D H D ' = 1 3 (OD // D’H) ⇒ I D I D ' = O D H D ' = 1 3
Mà J D / / N D ' ⇒ J D N D ' = I D I D ' = 1 3
Có N D ' = N C '
J D = K B = K B ' ⇒ F B ' C N = 1 3 = B ' E E C = 1 3