Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{BD'}=\overrightarrow{BA}+\overrightarrow{AD}+\overrightarrow{DD'}=-\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA'}\)
\(=-\overrightarrow{a}+\overrightarrow{b}+\overrightarrow{c}\)

\(\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}\Rightarrow\overrightarrow{BC}=\overrightarrow{AC}-\overrightarrow{AB}=\overrightarrow{b}-\overrightarrow{a}\)
Theo Talet: \(\dfrac{A'K}{IK}=\dfrac{B'I}{A'D'}=\dfrac{1}{2}\Rightarrow A'K=\dfrac{2}{3}A'I\)
\(\Rightarrow\overrightarrow{A'K}=\dfrac{2}{3}\overrightarrow{A'I}=\dfrac{2}{3}\left(\overrightarrow{A'B'}+\overrightarrow{B'I}\right)=\dfrac{2}{3}\left(\overrightarrow{A'B'}+\dfrac{1}{2}\overrightarrow{B'C'}\right)\)
\(=\dfrac{2}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{BC}=\dfrac{2}{3}\overrightarrow{a}+\dfrac{1}{3}\left(\overrightarrow{b}-\overrightarrow{a}\right)=\dfrac{1}{3}\overrightarrow{a}+\dfrac{1}{3}\overrightarrow{b}\)
\(\Rightarrow\overrightarrow{DK}=\overrightarrow{DD'}+\overrightarrow{D'A'}+\overrightarrow{A'K}=\overrightarrow{AA'}-\overrightarrow{BC}+\overrightarrow{A'K}\)
\(=\overrightarrow{c}-\left(\overrightarrow{b}-\overrightarrow{a}\right)+\dfrac{1}{3}\overrightarrow{a}+\dfrac{1}{3}\overrightarrow{b}\)
\(=\dfrac{4}{3}\overrightarrow{a}-\dfrac{2}{3}\overrightarrow{b}+\overrightarrow{c}\)

\(\overrightarrow{b}-\overrightarrow{c}+\overrightarrow{d}=\overrightarrow{AB}-\overrightarrow{AC}+\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\overrightarrow{CA}+\overrightarrow{BC}=\overrightarrow{CB}+\overrightarrow{BC}\)
\(=\overrightarrow{0}\)

\(\overrightarrow{AC'}+\overrightarrow{CA'}+\overrightarrow{BD'}+\overrightarrow{DB'}\)
\(=2\left(\overrightarrow{OC'}+\overrightarrow{OA'}\right)+2\left(\overrightarrow{OD'}+\overrightarrow{OB'}\right)\)
\(=2.\left(-2\overrightarrow{OI}\right)+2.\left(-2\overrightarrow{OI}\right)\)
\(=-4.2\overrightarrow{OI}\)
\(\Rightarrow2\overrightarrow{OI}=-\dfrac{1}{4}\left(\overrightarrow{u}+\overrightarrow{v}+\overrightarrow{x}+\overrightarrow{y}\right)\)
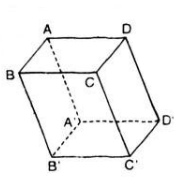

\(\overrightarrow{A'C}=\overrightarrow{A'A}+\overrightarrow{AC}=-\overrightarrow{AA'}+\overrightarrow{AB}+\overrightarrow{AD}=\overrightarrow{a}+\overrightarrow{b}-\overrightarrow{c}\)