Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

A B C D E F G H
a) Xét tam giác ADB có:
\(\frac{AE}{AB}=\frac{AH}{AD}\left(gt\right)\)
\(\Rightarrow HE//DB\left(1\right)\)( định lý Ta-let đảo )
Xét tam giác CDB có:
\(\frac{CF}{CB}=\frac{CG}{CD}\left(gt\right)\)
\(\Rightarrow GF//BD\left(2\right)\)
Từ (1) và (2) \(\Rightarrow HE//GF\)
CMTT\(HG//EF\)( cùng // AC)
Xét tứ giác EFGH có:
\(\hept{\begin{cases}HE//GF\left(cmt\right)\\HG//EF\left(cmt\right)\end{cases}\Rightarrow EFGH}\)là hình bình hành (dhnb)
b)
Đặt\(\frac{AE}{AB}=\frac{AH}{AD}=\frac{CF}{CB}=\frac{CG}{CD}=k\)
Xét tam giác ADB có:
\(HE//BD\left(gt\right)\)
\(\Rightarrow\frac{HE}{BD}=\frac{AE}{AB}\)( hệ quả của định lý Ta-let)
\(\Rightarrow\frac{HE}{BD}=k\)( vì \(\frac{AE}{AB}=k\))
\(\Rightarrow HE=k.BD\)
Xét tam giác ABC có:
\(EF//AC\left(cmt\right)\)
\(\Rightarrow\frac{EF}{AC}=\frac{BE}{BA}\)( hệ quả của định lý Ta-let)
\(\Rightarrow\frac{EF}{AC}=\frac{AB-AE}{BA}=1-k\)
\(\Rightarrow EF=\left(1-k\right)AC\)
\(P_{EFGH}=2\left(HE+EF\right)\)
\(=2\left[k.BD+\left(1-k\right)AC\right]\)
\(=2AC\)không đổi ( AC=BD do ABCD là hình chữ nhật )
Vậy chu vi của hbh EFGH có giá trị không đổi

Câu 12. Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình chữ nhật. B. Hình thoi. C. Hình bình hành. Câu 13. Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là: | D. Hình vuông. |
A. 4cm. B. 7cm. C. 14cm. Câu 14. Cho hình vuông có chu vi 32 cm. Độ dài cạnh hình vuông là: | D. 8cm. |
A. 10cm. B. 15cm. C. 5cm. | D. 8cm. |
Câu 12. Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình chữ nhật. B. Hình thoi. C. Hình bình hành. D. Hình vuông.
Câu 13. Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là:
A. 4cm. B. 7 cm. C. 14cm. D. 8cm.
Câu 14. Cho hình vuông có chu vi 32 cm. Độ dài cạnh hình vuông là:
A. 10cm. B. 15cm. C. 5cm. D. 8 cm

a: AE=EB=AB/2
CG=GD=CD/2
mà AB=CD
nên AE=EB=CG=GD
AH=HD=AD/2
BF=FC=BC/2
mà AD=BC
nên AH=HD=BF=FC
b: Xét ΔAHE và ΔCFG có
AH=CF
góc A=góc C
AE=CG
=>ΔAHE=ΔCFG
c: Xét ΔEBF và ΔGDH có
EB=GD
góc B=góc D
BF=DH
=>ΔEBF=ΔGDH
=>GH=EF
d: Xét tứ giác EHGF có
EH=FG
EF=GH
=>EHGF là hình bình hành

A B C D E F G H
Xét \(\Delta ADB\):
\(AE=EB\left(gt\right)\)
\(HD=HA\left(gt\right)\)
\(\Rightarrow HE\)là đường trung binh cũa \(\Delta ADB\).
\(\Rightarrow HE\)//\(DB\)và \(HE=\frac{1}{2}DB\left(1\right)\)
Xét \(\Delta CDB:\)
\(FB=FC\left(gt\right)\)
\(GC=GD\left(gt\right)\)
\(\Rightarrow GF\) là dường trung bình của \(\Delta CBD\).
\(\Rightarrow GF\)//\(DB\)và \(GF=\frac{1}{2}DB\left(2\right)\)
Từ \(\left(1\right)\left(2\right)\Rightarrow\)\(HE\)//\(GF\)và \(HE=GF\)
Vậy tứ giác \(EFGH\)là hình bình hành.
b) Xét \(\Delta AEH\)và \(\Delta EBF\):
\(AE=EB\left(gt\right)\)
Góc A = Góc B = 90o (ABCD là hình chữ nhật)
\(AD=BC\Rightarrow\frac{1}{2}AD=\frac{1}{2}BC\Rightarrow AH=BF\)
\(\Rightarrow\Delta AEH=\Delta EBF\left(c.g.c\right)\)
\(\Rightarrow HE=HF\)
mà tứ giác EFGH là hình bình hành.
Vậy hình bình hành \(EFGH\)là hình thoi.

AE//CG, AE = CG nên AECG là hình bình hành ⇒ O là trung điểm của EG. Tương tự O là trung điểm của HF.

Hình vẽ đây :
YAX34P43.jpg (578×558)
Bài làm để Cô Quản Lý giúp đỡ nhá bn :)
Hc tốt
A B C D E F H G I
a) Gọi I là trung điểm AF
=> AI = IF = FD = 1/3 AD = 1/3 BC = BE
Mà AI//BE ( vì AD //BC)
=> ABEI là hình bình hành.
=> EI //AB (1)
Xét tam giác AFH có: IE//AG ( theo (1) ) và I là trung điểm AF
=> E là trung điểm FG => EG = EF
Dễ dàng chứng minh được \(\Delta FHD=\Delta EGB\)=> HF = GE
=> GE = HF = EF
b ) DF = 1/3 DA => AF= 2/3 DA
BE = 1/3 BC => EC = 2/3 BC
Vì ABCD là hình bình hành => DA = BC => AF = EC
Mà AF// EC ( vì AD //BC )
=> AF//=EC
=> AECF là hình bình hành.

Từ các hệ Thức trên ta dễ dàng có HE//BD//FG(1)
Suy ra \(\frac{AE}{AB}=\frac{AH}{AD}=\frac{CF}{CB}=\frac{CG}{CD}=\frac{HE}{BD}=\frac{FG}{BD}=k\Rightarrow HE=FG\)(2)
Từ (1) và (2) có ĐPCM
b/Ta cx dễ dàng chứng minh đc \(\frac{EG}{AC}=\frac{HF}{AC}=\)\(\frac{EB}{AB}=\frac{AB}{AB}-\frac{AE}{AB}=1-k\)
Ta thấy HE,FG tỉ lệ thuận BD =k
EG,HF tỉ lệ thuận AC =1-k
Mà AC,BD cố định suy ra Các cạnh của HBH cố định, suy ra Chu vi cx cố định
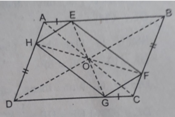
A B C D E F G H a) Xét ΔABD có:\(\dfrac{AE}{AB}=\dfrac{AH}{AD}\)
⇒ HE//DB (đl Talet đảo) (1)
Xét ΔBCD có:\(\dfrac{BF}{BC}=\dfrac{CG}{CD}\)
⇒ FG//BD (đl Talet đảo) (2)
Từ (1)(2)⇒HE//FG (*)
Xét ΔADC có: \(\dfrac{AH}{AD}=\dfrac{DG}{DC}\)
⇒ HG//AC (đl Talet đảo) (3)
Xét ΔABC có: \(\dfrac{AE}{AB}=\dfrac{BF}{BC}\)
⇒ EF//AC (đl Talet đảo) (4)
Từ (3)(4)⇒EF//HG (**)
Từ (*)(**)⇒ Tứ giác EFGH là hbh.
b) Câu này mk ko hiểu đề bài cho lắm