Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

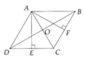
a) Chứng minh được MBPD và BNDQ đều là hình bình hành Þ ĐPCM.
b) Áp dụng định lý Talet đảo cho DABD và DBAC tacos MQ//BD và MN//AC.
Mà ABCD là hình thoi nên AC ^ BD Þ MQ ^ MN
MNPQ là hình chữ nhật vì có các góc ở đỉnh là góc vuông

Tứ giác có thể là hình vuông, chữ nhật phải không bạn?
P/s: Hỏi thôi chớ không trả lời đâu :D

a: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MQ//NP và MQ=NP
hay MQPN là hình bình hành

a:
ABCD là hình thoi
=>AC vuông góc BD tại trung điểm của mỗi đường
=>AC vuông góc BD tại O và O là trung điểm chung của AC và BD
AM+MB=AB
PC+PD=DC
mà AM=PC và AB=DC
nên MB=PD
Xét tứ giác BMDP có
BM//DP
BM=DP
Do đó: BMDP là hình bình hành
b: Xét tứ giác AQCN có
AQ//CN
AQ=CN
Do đó: AQCN là hình bình hành
=>AC cắt QN tại trung điểm của mỗi đường
=>O là trung điểm của QN
=>N,O,Q thẳng hàng
c: Xét ΔABD có AM/AB=AQ/AD
nên MQ//BD
=>MQ vuông góc AC
Xét ΔABC có
BM/BA=BN/BC
nên MN//AC
=>MQ vuông góc MN
BMDP là hình bình hành
=>BD cắt MP tại trung điểm của mỗi đường
=>O là trung điểm của MP
Xét tứ giác MNPQ có
O là trung điểm chung của MP và NQ
góc NMQ=90 độ
Do đó: MNPQ là hình chữ nhật

a) Hai tam giác OAM và OCP có: OA = OC
ˆOAM=ˆOCP ( AB song song CD )
AM = CP
Suy ra 2 tam giác này bằng nhau => ˆMOA=ˆCOP => M, O, P thẳng hàng.
Tương tự suy ra N, O, Q thẳng hàng
b) Do BM = BN, BA = BC nên theo định lí Thales đảo suy ra MN song song AC + PQ song song AC => MN song song PQ.
Tương tự MQ song song NP. Mà ta lại có AC vuông góc với BD => MNPQ là hình chữ nhật.