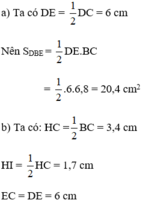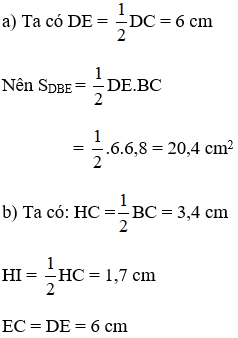Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

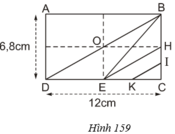
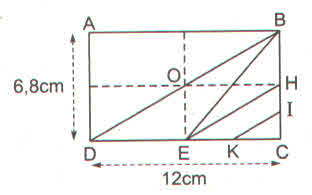
a)Ta có: DE=12DC(=12.12=6(cm)DE=12DC(=12.12=6(cm)
Nên SDBE=12.DE.BC=12.6.6,8=20,4(cm3)SDBE=12.DE.BC=12.6.6,8=20,4(cm3)
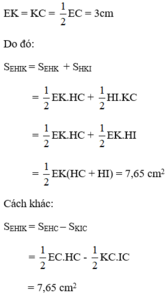
b)Ta có : HC=12BC=12.6,8=3,4(cm)HC=12BC=12.6,8=3,4(cm)
HI=12HC=12.3,4=1,7(cm)HI=12HC=12.3,4=1,7(cm)
EC = DE = 6cm
EK=KC=12EC=12.6=3(cm)EK=KC=12EC=12.6=3(cm)
Do đó SEHIK=SEHK+SHKI=12EK.HC+12HI.KCSEHIK=SEHK+SHKI=12EK.HC+12HI.KC
= 12EK.HC+12EK.HI=12EK(HC+HI)12EK.HC+12EK.HI=12EK(HC+HI)
SEHIK=12.3.(3,4+1,7)=12.3.5,1=7,65(cm2)SEHIK=12.3.(3,4+1,7)=12.3.5,1=7,65(cm2)
Cách khác:
SEHIK=SEHC−SKIC=12EC.HC−12KC.ICSEHIK=SEHC−SKIC=12EC.HC−12KC.IC
= 12.6.3,4−12.3.1,712.6.3,4−12.3.1,7
= 10,2−2,55=7,65(cm2)

a: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình
=>MQ//BD và MQ=BD/2(1)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình
=>NP//BD và NP=BD/2(2)
Từ (1) và (2) suy ra MQ//NP và MQ=NP
hay MQPN là hình bình hành

a: Xét hình thang ABCD có
M là trung điểm của AB
N là trung điểm của CD
Do đó: MN là đường trung bình của hình thang ABCD
Suy ra: \(MN=\dfrac{AD+BC}{2}=14\left(cm\right)\)
a) xét hình thang ABCD có:
M là trung điểm của AB
N là trung điểm của DC
\(\Rightarrow\) MN là đường trung bình của hình thang ABCD
\(\Rightarrow MN=\dfrac{AD+BC}{2}=\dfrac{16+12}{2}=\dfrac{28}{2}=14cm\)