Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
Lời giải.
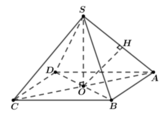
Xét hình chóp tứ giác đều S.ABCD, đặt AB =x, SO =h. Với O là tâm của hình vuông ABCD ⇒ S O ⊥ ( A B C D ) . Qua O kẻ đường thẳng OH vuông góc với SA với H ∈ SA
Ta có
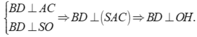
Suy ra OH là đoạn vuông góc chung của SA và BD
Theo bài ra, ta có
![]()
Tam giác SAO vuông tại O, có đường cao OH suy ra
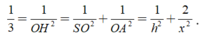
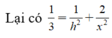
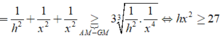
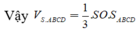
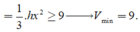

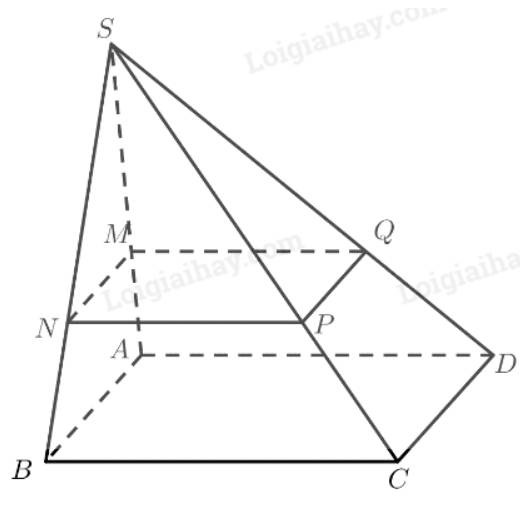
Qua \(M\) dựng đường thẳng song song với \(AB\), cắt \(SB\) tại \(N\).
Qua \(N\) dựng đường thẳng song song với \(BC\), cắt \(SC\) tại \(P\).
Qua \(M\) dựng đường thẳng song song với \(AD\), cắt \(SD\) tại \(Q\).
Ta có:
\(\left. \begin{array}{l}MN\parallel AB\\AB \subset \left( {ABCD} \right)\end{array} \right\} \Rightarrow MN\parallel \left( {ABCD} \right)\)
\(\left. \begin{array}{l}MQ\parallel AD\\AD \subset \left( {ABCD} \right)\end{array} \right\} \Rightarrow MQ\parallel \left( {ABCD} \right)\)
\(\left. \begin{array}{l}MN\parallel \left( {ABCD} \right)\\MQ\parallel \left( {ABCD} \right)\\MN,MQ \subset \left( \alpha \right)\end{array} \right\} \Rightarrow \left( {MNPQ} \right)\parallel \left( {ABCD} \right)\)
\( \Rightarrow \frac{{{S_{MNPQ}}}}{{{S_{ABC{\rm{D}}}}}} = {\left( {\frac{{MN}}{{AB}}} \right)^2}\)
Ta có: \({S_{ABC{\rm{D}}}} = A{B^2} = {10^2} = 100\)
\(MN\parallel AB \Rightarrow \frac{{MN}}{{AB}} = \frac{{SM}}{{SA}} = \frac{2}{3}\)
\( \Rightarrow \frac{{{S_{MNPQ}}}}{{{S_{ABC{\rm{D}}}}}} = {\left( {\frac{2}{3}} \right)^2} = \frac{4}{9} \Rightarrow {S_{MNPQ}} = \frac{4}{9}{S_{ABC{\rm{D}}}} = \frac{4}{9}.100 = \frac{{400}}{9}\)
Chọn A.

Gọi N là trung điểm AB \(\Rightarrow\left\{{}\begin{matrix}ON\perp AB\\SO\perp AB\end{matrix}\right.\) \(\Rightarrow AB\perp\left(SON\right)\)
Từ O kẻ \(OH\perp SN\) (H thuộc SN) \(\Rightarrow OH\perp\left(SAB\right)\Rightarrow OH=d\left(O;\left(SAB\right)\right)\)
\(ON=\dfrac{1}{2}AD=\dfrac{a}{2}\) ; \(SO=\dfrac{a\sqrt{2}}{2}\)
Hệ thức lượng: \(OH=\dfrac{SO.ON}{\sqrt{SO^2+ON^2}}=\dfrac{a\sqrt{6}}{6}\)
Lại có: M là trung điểm OD \(\Rightarrow OM=\dfrac{1}{2}OD\Rightarrow BM=\dfrac{3}{2}OB\)
\(\Rightarrow d\left(M;\left(SAB\right)\right)=\dfrac{3}{2}d\left(O;\left(SAB\right)\right)=\dfrac{3}{2}.\dfrac{a\sqrt{6}}{6}=\dfrac{a\sqrt{6}}{4}\)

Gọi O là tâm đáy \(\Rightarrow\) O là trung điểm BD và AC
Trong mp ((SAC), nối SO cắt AM tại I
\(\Rightarrow I=AM\cap\left(SBD\right)\)
Ta có M là trung điểm SC, O là trung điểm AC
\(\Rightarrow\) I là trọng tâm tam giác SAC
\(\Rightarrow\dfrac{IA}{AM}=\dfrac{2}{3}\Rightarrow\dfrac{MA}{IA}=\dfrac{3}{2}\)

b: SA vuông góc (ABCD)
=>SA vuông góc AC
=>ΔSAC vuông tại A
c: AC=căn a^2+a^2=a*căn 2
=>SC=căn SA^2+AC^2=a*căn 5
SD=căn SA^2+AD^2=2a
Vì DS^2+DC^2=SC^2
nên ΔSDC vuông tại D

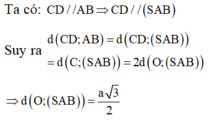


Đáp án A
Gọi O là tâm của đáy. Gọi a>0 là khoảng cách giữa SA và DB.