Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
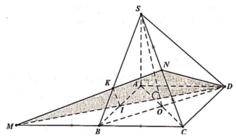
Gọi ![]()
Khi đó góc giữa 2 mặt phẳng (SBD) và (ABCD) bằng 45o![]()
Ta có: ∆BAD đều ![]()
Thể tích khối chóp S.ABCD bằng: 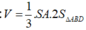
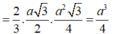
Ta có: N là trung điểm SC nên 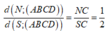
Thể tích khối chóp N.MCD bằng thể tích khối chóp N.ABCD bằng: ![]()
Ta có K là trọng tâm tam giác SMC
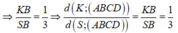
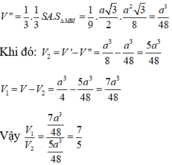

Chọn C
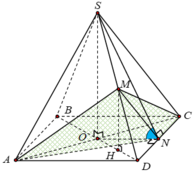
Gọi O là tâm của hình vuông ABCD.
Góc giữa cạnh bên (SAB) và mặt đáy là góc S N O ^ = 60 o
Xét tam giác SNO, ta có SO = NO tan600 = a 3
Lại có M là trung điểm của SD nên:
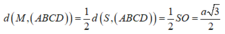
N là trung điểm của CD nên S ∆ A C N = 1 4 S A B C D = 1 4 4 a 2 = a 2
Do đó, thể tích khối MACN là
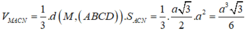

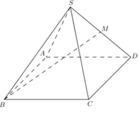
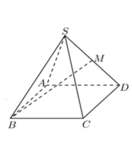
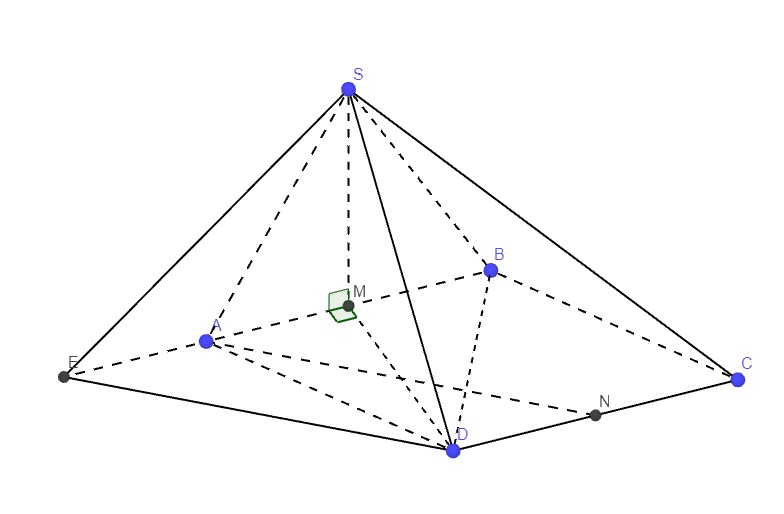
Gọi E là điểm đối xứng M qua A
\(\Rightarrow ANDE\) là hình bình hành (cặp cạnh đối AE và DN song song và bằng nhau)
\(\Rightarrow AN||DE\Rightarrow\) góc giữa AN và SD bằng góc giữa SD và DE
Do tam giác ABD đều \(\Rightarrow MD\perp AB\) \(\Rightarrow\Delta MDE\) vuông tại M
Do tam giác SAB đều \(\Rightarrow SM\perp AB\)
Mà \(\left(SAB\right)\perp\left(ABCD\right)\Rightarrow SM\perp\left(ABCD\right)\)
\(\Rightarrow\) Các tam giác SMD, SME vuông tại M
\(SM=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác SAB đều)
\(MD=\dfrac{AB\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác ABD đều)
\(ME=2AM=AB=a\)
Pitago:
\(SD=\sqrt{SM^2+MD^2}=\dfrac{a\sqrt{6}}{2}\)
\(SE=\sqrt{SM^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(ED=\sqrt{MD^2+ME^2}=\dfrac{a\sqrt{7}}{2}\)
\(\Rightarrow cos\widehat{SDE}=\dfrac{SD^2+ED^2-SE^2}{2SD.ED}=\dfrac{\sqrt{42}}{14}\)
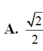
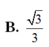
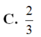
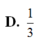

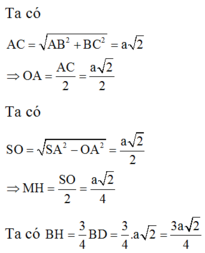
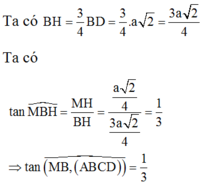


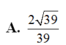
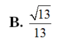
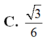
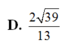





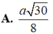
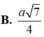
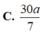
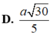

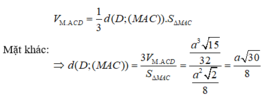

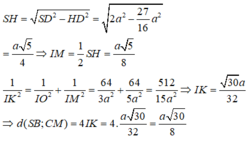
đáp án D
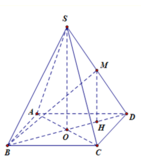
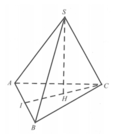
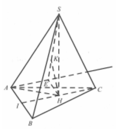
Do S.ABCD là hình chóp tứ giác đều ⇒ S O ⊥ ( A B C D ) .
Gọi K là trung điểm OD
MK sẽ là đường trung bình trong tam giác ∆ S O D
⇒ M K ⊥ ( A B C D )
⇒ tan M B K = M K B K
⇒ tan M B K = M K B K = 1 3
Chọn đáp án D