Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: (SB;(ABCD))=(BS;BA)=góc SBA
b: (SO;(ABCD))=(OS;OA)=góc SOA
c: (SC;(SAD))=(SC;SD)

a: Qua S kẻ đường Sx song song SD
=>Sx vuông góc SA
SC vuông góc CD
=>SC vuông góc Sx
((SAB);(SCD))=góc ASC
b: (SBD) căt (SAB)=SB
Kẻ DA vuông góc AB
mà DA vuông góc SA
nên DA vuông góc (SAB)
=>DA vuông góc SB
Kẻ AK vuông góc SB
=>((SBD);(SAB))=góc AKD
c: (SBC) giao (SCD)=SC
Kẻ BH vuông góc SC
Qua H kẻ HF//CD
=>HF vuông góc SC
=>((SBC);(SCD))=góc BHF

a: (SBD) giao (ABCD)=BD
AB vuông góc BD
SB vuông góc BD
=>góc cần tìm là góc SBA

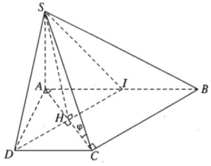
a) Ta có:
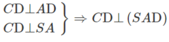
⇒ (SCD) ⊥ (SAD)
Gọi I là trung điểm của đoạn AB. Ta có AICD là hình vuông và IBCD là hình bình hành. Vì DI // CB và DI ⊥ CA nên AC ⊥ CB. Do đó CB ⊥ (SAC).
Vậy (SBC) ⊥ (SAC).
b) Ta có:
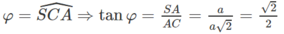
c) 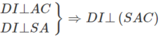
Vậy (α) là mặt phẳng chứa SD và vuông góc với mặt phẳng (SAC) chính là mặt phẳng (SDI). Do đó thiết diện của (α) với hình chóp S.ABCD là tam giác đều SDI có chiều dài mỗi cạnh bằng a√2. Gọi H là tâm hình vuông AICD ta có SH ⊥ DI và 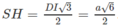 .
.
Tam giác SDI có diện tích:
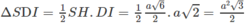

a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\AD\perp CD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
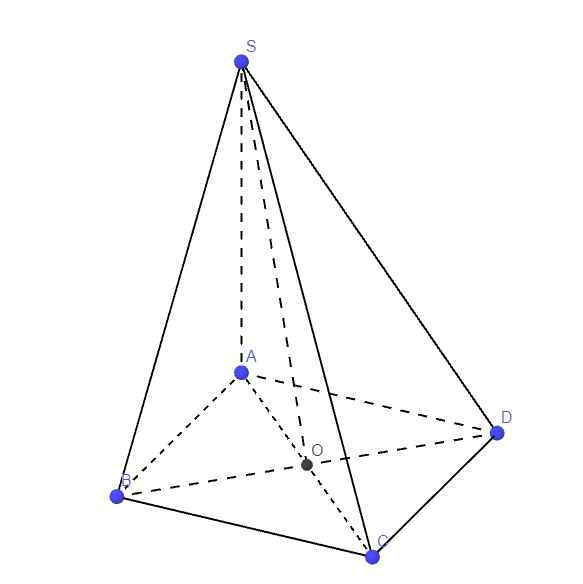
b.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp BD\\BD\perp AC\left(\text{hai đường chéo hình vuông}\right)\end{matrix}\right.\) \(\Rightarrow BD\perp\left(SAC\right)\)
Mà \(SO\in\left(SAC\right)\Rightarrow BD\perp SO\)
c.
\(SA\perp\left(ABCD\right)\Rightarrow AO\) là hình chiếu vuông góc của SO lên (ABCD)
\(\Rightarrow\widehat{SOA}\) là góc giữa SO và (ABCD)
\(AO=\dfrac{1}{2}AC=\dfrac{a\sqrt{2}}{2}\)
\(tan\widehat{SOA}=\dfrac{SA}{AO}=\sqrt{6}\Rightarrow\widehat{SOA}\approx67^047'\)

a.
\(\left\{{}\begin{matrix}SE\perp\left(EFGH\right)\\GF\in\left(EFGH\right)\end{matrix}\right.\) \(\Rightarrow SE\perp GF\)
b.
\(\left\{{}\begin{matrix}SE\perp\left(EFGH\right)\Rightarrow SE\perp GH\\GH\perp EH\left(\text{EFGH là hình vuông}\right)\end{matrix}\right.\)
\(\Rightarrow GH\perp\left(SHE\right)\)
c.
\(\left\{{}\begin{matrix}SE\perp\left(EFGH\right)\Rightarrow SE\perp HE\\HE\perp EF\left(\text{EFGH là hình vuông}\right)\end{matrix}\right.\)
\(\Rightarrow HE\perp\left(SEF\right)\)
c.
\(\left\{{}\begin{matrix}SE\perp\left(EFGH\right)\\HE\in\left(EFGH\right)\end{matrix}\right.\) \(\Rightarrow SE\perp HE\)
\(\Rightarrow\) Góc giữa SE và HE là 90 độ
d.
Không thể xác định cụ thể được số đo góc giữa 2 đường thẳng này, do nó phụ thuộc vào độ dài đoạn SE. Góc giữa 2 đường thẳng này bằng góc SGH do EF song song GH
(Góc giữa SG và HF thì xác định được)