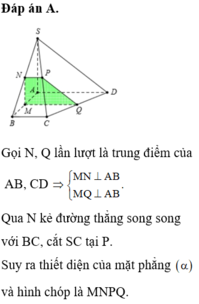
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
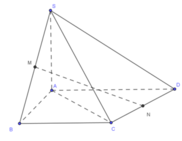
Kẻ CN
⊥
AB ta dễ dàng tính được 
=> tam giác ADC vuông tại C. Từ đó NC ⊥ (SAC)
Gọi O là trung điểm của AC, dễ dàng cm được BD ⊥ (SAC)
=> MK ⊥ (SAC). vơí K là trung điểm của SO, từ đó KC là hc của MN lên .
Ta kẻ KZ ⊥ AC
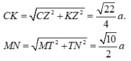
với T là trung điểm của AB.
Gọi α là góc tạo với MN và (SAC)
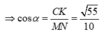
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
\(AC=\sqrt{AD^2+CD^2}=a\sqrt{2}\)
\(BC=\sqrt{BE^2+CE^2}=a\sqrt{2}\)
\(\Rightarrow AC^2+BC^2=AB^2\Rightarrow AC\perp BC\)
\(\Rightarrow BC\perp\left(SAC\right)\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\)
b.
\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}=30^0\Rightarrow SA=AD.tan30^0=\dfrac{a\sqrt{3}}{3}\)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Qua S kẻ đường thẳng d song song AD
Do \(AD||CE\) \(\Rightarrow\) d là giao tuyến (SAD) và (SCE)
Mà \(d\perp\left(SAB\right)\Rightarrow\widehat{ASE}\) là góc giữa (SAD) và (SCE)
\(AE=\dfrac{AB}{2}=a\)
\(tan\widehat{ASE}=\dfrac{AE}{SA}=\sqrt{3}\Rightarrow\widehat{ASE}=60^0\)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là giao điểm AC và DI
I là trung điểm AB \(\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC\)
\(\Rightarrow AICD\) là hình bình hành
Mà \(\widehat{A}=90^0\Rightarrow AICD\) là hình chữ nhật
\(AI=AD=a\) (hai cạnh kề bằng nhau) \(\Rightarrow AICD\) là hình vuông
\(\Rightarrow AC\perp DI\) tại E
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)\)
Mà \(DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}\) là góc giữa (SDI) và (ABCD)
\(AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'\)
Ta có \(\frac{d\left(A,\left(SCD\right)\right)}{d\left(M,\left(SCD\right)\right)}=2\Rightarrow d=\left(m,\left(SCD\right)\right)=\frac{1}{2}d\left(A,\left(SCD\right)\right)\)
Dễ thấy AC _|_ CD, SA _|_ CD dựng AH _|_ SA => AH _|_ (SCD)
Vậy d(A,(SCD))=AH
Xét tam giác vuông SAC (A=1v) có \(\frac{1}{AH^2}=\frac{1}{AC^2}+\frac{1}{AS^2}\Rightarrow AH=\frac{a\sqrt{6}}{3}\)
Vậy suy ra \(d\left(M,\left(SCD\right)\right)=\frac{a\sqrt{6}}{3}\)
.jpg)
là trọng tâm tam giác SAE.
Tứ diện AEND vuông tại đỉnh A nên
Vậy
a: \(AC=\sqrt{a^2+a^2}=a\sqrt{2}\)
(SC;(ABCD))=(CS;CA)=góc SCA
tan SCA=SA/AC=1/căn 2
=>góc SCA=35 độ
b:
Kẻ BH vuông góc AC tại H
(SB;SAC)=(SB;SH)=góc BSH
\(HB=\dfrac{a\cdot a}{a\sqrt{2}}=a\cdot\dfrac{\sqrt{2}}{2}\)
AH=AC/2=a*căn 2/2
=>\(SH=\sqrt{a^2+\dfrac{1}{2}a^2}=a\sqrt{\dfrac{3}{2}}\)
\(SH=\dfrac{a\sqrt{6}}{2};HB=\dfrac{a\sqrt{2}}{2};SB=a\sqrt{2}\)
\(cosBSH=\dfrac{SB^2+SH^2-BH^2}{2\cdot SB\cdot SH}=\dfrac{\sqrt{3}}{2}\)
=>góc BSH=30 độ
c: (SD;(SAB))=(SD;SA)=góc ASD
tan ASD=AD/AS=2
nên góc ASD=63 độ
Bạn kiểm tra lại đề,
1. ABCD là hình thang vuông tại A và B hay A và D? Theo dữ liệu này thì ko thể vuông tại B được (cạnh huyền DC nhỏ hơn cạnh góc vuông AB là cực kì vô lý)
2. SC và AC cắt nhau tại C nên giữa chúng không có khoảng cách. (khoảng cách bằng 0)
Nguyễn Việt Lâm
e xin loi a
ABCD là hình thang vuông tại A và D
còn đoạn sau khoảng cách giữa 2 đt SC và AC thì e kh biet no sai o đau
anh giup em vs ah
Bài này đặt ở khu vực lớp 12 mình còn giải (vì có thể sử dụng tọa độ hóa cực lẹ)
Còn lớp 11 thì dựng hình được, nhưng việc tính toán số liệu sau đó đúng là thảm họa.
