Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a: BD vuông góc AC
BD vuông góc SA
=>BD vuông góc (SAC)
=>(SBD) vuông góc (SAC)
b: BC vuông góc AB
BC vuông góc SA
=>BC vuông góc (SAB)
=>BC vuông góc AK
mà AK vuông góc SB
nên AK vuông góc (SBC)
Tuy nhiên đề cho giá trị cạnh AC với BC bị sai. Cạnh huyền AC (\(a\sqrt{3}\)) sao lại có giá trị nhỏ hơn cạnh góc vuông BC (2a) nhỉ?
Đề bài thiếu chi tiết định dạng điểm S nên không giải được (ví dụ phải thêm SA vuông góc mặt đáy hoặc gì đó tương tự)
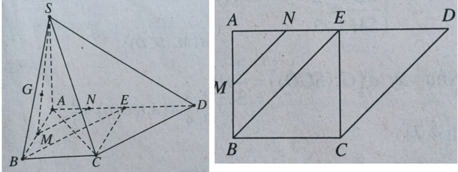
+ Xác định góc của SC với (SAD).
Hạ CE ⊥ AD, ta có E là trung điểm AD và CE ⊥ (SAD) nên ∠(CSE) = 30 o .
∠(CSE) cũng chính là góc giữa SC và mp(SAD).
Trong ΔCSE, ta có:
S E = C E . tan 60 o = a 3 ⇒ S A = S E 2 - A E 2 = 3 a 2 - a 2 = a 2 .
Nhận xét
Gọi M, N lần lượt là trung điểm của AB và AE.
Ta có MN // BE nên MN // CD. Như vậy MN // (SCD). Ta suy ra
d(M,(SCD)) = d(N,(SCD)).
Mà DN/DA = 3/4 nên d(N,(SCD)) = 3/4 d(A,(SCD))
+ Xác định khoảng cách từ A đến (SCD).
Vì vậy tam giác ACD vuông cân tại C nên CD vuông góc với AC.
CD ⊥ AC & CD ⊥ SA ⇒ CD ⊥ (SAC) ⇒ (SCD) ⊥ (SAC).
Hạ AH ⊥ SC, ta có AH ⊥ (SCD).
Do SA ⊥ (ABCD) ⇒ \(\left\{{}\begin{matrix}SA\perp AB\\SA\perp AC\\SA\perp BC\end{matrix}\right.\)
Mà BC ⊥ AC ⇒ BC ⊥ (SAC) ⇒ BC ⊥ SC và BC ⊥ AH
Do BC ⊥ AH và AH ⊥ SC ⇒ AH ⊥ (SBC) ⇒ AH ⊥ KH ⇒ \(\widehat{AHK}=90^0\)
ΔSAB và ΔSAC vuông tại A
Mà AH và AK lần lượt là đường cao của ΔSAB và ΔSAC
⇒ \(\left\{{}\begin{matrix}SA^2=SK.SB\\SA^2=SH.SC\end{matrix}\right.\)
⇒ SK . SB = SH . SC
⇒ \(\dfrac{SK}{SH}=\dfrac{SC}{SB}\) ⇒ ΔSKH \(\sim\) ΔSCB ⇒ \(\widehat{SKH}=\widehat{SCB}=90^0\)
⇒ HK ⊥ SB
Mà AK⊥ SB
⇒ ((SAB),(SCB)) = (AK,AH) = \(\widehat{KAH}\) = 450 (đây là góc nhọn, vì \(\widehat{AHK}=90^0\))
⇒ ΔHAK vuông cân tại H ⇒ AK = \(\sqrt{2}AH\)
Ta có : \(\dfrac{S_{SAC}}{S_{SAB}}=\dfrac{\dfrac{1}{2}.AH.SC}{\dfrac{1}{2}AK.SB}=\dfrac{\dfrac{1}{2}.SA.AC}{\dfrac{1}{2}.SA.AB}\)
⇒ \(\dfrac{AH.SC}{AK.SB}=\dfrac{SA.AC}{SA.AB}\)
⇒ \(\dfrac{1}{\sqrt{2}}\) . \(\dfrac{SC}{SB}\) = \(\dfrac{AC}{AB}\). Mà AC = a và AB = 2a
⇒ \(\dfrac{1}{\sqrt{2}}\)\(\dfrac{SC}{SB}\) = \(\dfrac{1}{2}\) ⇒ \(\dfrac{SC^2}{SB^2}\) = \(\dfrac{1}{2}\) . Mà SB2 - SC2 = BC2 = 3a2
⇒ \(\left\{{}\begin{matrix}SC^2=3a^2\\SB^2=6a^2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}SB=a\sqrt{6}\\SC=a\sqrt{3}\end{matrix}\right.\) ⇒ SA = a\(\sqrt{2}\)
Từ đó ta tính được SH = \(\dfrac{2a\sqrt{3}}{3}\) và SK = \(\dfrac{a\sqrt{6}}{3}\)
Gọi M là trung điểm của SB thì ta có CM // HK (cùng vuông góc với SB)
Khoảng cách từ HK đến AC bằng khoảng cách từ HK đến (AMC)
a) Gọi O là tâm hình vuông ABCD , dễ thấy I, O, K thẳng hàng. Vì K là trung điểm của BC nên SK ⊥ BC.
Ta có 
Do đó (SBC) ⊥ (SIK)
b) Hai đường thẳng AD và SB chéo nhau. Ta có mặt phẳng (SBC) chứa SB và song song với AD. Do đó khoảng cách giữa AD và SB bằng khoảng cách giữa AD và mặt phẳng (SBC).
Theo câu a) ta có (SIK) ⊥ (SBC) theo giao tuyến SK và khoảng cách cần tìm là IM, trong đó M là chân đường vuông góc hạ từ I tới SK. Dựa vào hệ thức IM. SK = SO. IK
ta có 
Ta lại có:
Do đó:
Vậy khoảng cách giữa hai đường thẳng AD và SB là bằng 
Đáp án B.
Vẽ đường thẳng d qua B và song song với AC.
Gọi K, I lần lượt là hình chiếu của H trên d và SB, L là hình chiếu của H trên SK.
a. Ta có : \(\begin{cases}AB\perp BC\left(ABCDvuong\right)\\SA\perp BC\left(SA\perp\left(ABCD\right)\right)\end{cases}\) \(\Rightarrow BC\perp\left(SAB\right)\) mà \(SB\subset\left(SAB\right)\) nên \(BC\perp SB\) Vậy \(\Delta SBC\left(\perp B\right)\)
tương tự ta có : \(\begin{cases}SA\perp DC\\AD\perp DC\end{cases}\) \(\Rightarrow DC\perp\left(SAD\right)\) mà \(SD\subset\left(SAD\right)\) nên \(SD\perp DC\) Vậy \(\Delta SDC\left(\perp D\right)\)
ta có \(SA\perp AD\) nên \(\Delta SAD\left(\perp A\right)\)
Có \(SA\perp AB\) nên \(\Delta SAB\left(\perp A\right)\)
b. Ta có : \(\begin{cases}AC\perp BD\\SA\perp BD\end{cases}\) \(\Rightarrow BD\perp\left(SAC\right)\) mà \(BD\subset\left(SBD\right)\) nên \(\left(SAC\right)\perp\left(SBD\right)\)
Bạn kiểm tra lại đề,
1. ABCD là hình thang vuông tại A và B hay A và D? Theo dữ liệu này thì ko thể vuông tại B được (cạnh huyền DC nhỏ hơn cạnh góc vuông AB là cực kì vô lý)
2. SC và AC cắt nhau tại C nên giữa chúng không có khoảng cách. (khoảng cách bằng 0)
Nguyễn Việt Lâm
e xin loi a
ABCD là hình thang vuông tại A và D
còn đoạn sau khoảng cách giữa 2 đt SC và AC thì e kh biet no sai o đau
anh giup em vs ah