Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Mặt phẳng cách đều 5 điểm là mặt phẳng mà khoảng cách từ 5 điểm đó đến mặt phẳng là bằng nhau.
Có 5 mặt phẳng thỏa mãn là:
+ Mặt phẳng đi qua trung điểm của AB,CD và song song với SBC .
+ Mặt phẳng đi qua trung điểm của AB,CD và song song với SAD .
+ Mặt phẳng đi qua trung điểm của AD,BC và song song với SAB .
+ Mặt phẳng đi qua trung điểm của AD,BC và song song với SCD .
+ Mặt phẳng đi qua trung điểm của SA,SB,SC,SD.

Đáp án B.
Phương pháp: Tính độ dài đoạn thẳng IM với I là tâm mặt cầu.
Tham số hóa tọa độ điểm M, sau đó dựa vào độ dài IM để tìm điểm M.
Cách giải : Mặt cầu (S) có tâm I(1;2; – 3) bán kính R = 3 3
Đặt MA = MB = MC = a
Tam giác MAB đều => AB = a
Tam giác MBC vuông tại M => BC = a 2
Tam giác MCA có C M A ^ = 120 0 => AC = a 3
Xét tam giác ABC có A B 2 + B C 2 = A C 2 => ∆ABC vuông tại B
=>∆ABC ngoại tiếp đường tròn nhỏ có đường kính AC
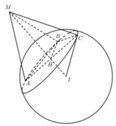
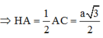
Xét tam giác vuông IAM có:
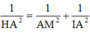
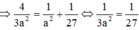
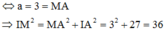
![]()
![]()
![]()
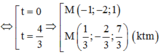
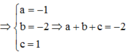

Đáp án D
Tồn tại 5 mặt phẳng thỏa mãn đề bài là:
- Mp đi qua trung điểm AD,BC,SC,SD
- Mp đi qua trung điểm CD,AB,SC,SB
- Mp đi qua trung điểm AD,BC,SB,SA
- Mp đi qua trung điểm CD,AB,SA,SD
- Mp đi qua trung điểm SA,SB,SC,SD

Đáp án B
Phương pháp:
Gọi các trung điểm của các cạnh bên và các cạnh đáy.
Tìm các mặt phẳng cách đều 5 điểm S, A, B, C, D.
Cách giải:
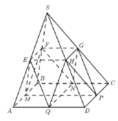
Gọi E; F; G; H lần lượt là trung điểm của SA, SB, SC, SD và M, N, P, Q lần lượt là trung điểm của AB, BC, CD, DA .
Ta có thể tìm được các mặt phẳng cách đều 5 điểm S, A, B, C, D là (EFGH); (EFNQ); (GHQN); (FGPM); (EHPM)

Đáp án D
Phương pháp: Đưa khoảng cách từ M đến (SAC) về khoảng cách từ H đến (SAC).
Cách giải: Gọi H là trung điểm của AB ta có SH ⊥ (ABCD)
Ta có (SC;(ABCD)) = (SC;HC) = Góc SCH = 45 0
=>∆SHC vuông cân tại H => 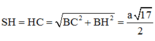
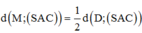
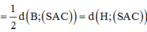
Trong (ABD) kẻ HI ⊥ AC,trong (SHI) kẻ HK ⊥ SI ta có:
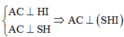
![]()
![]()
Ta có ∆AHI: ∆A CB(g.g) => 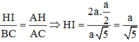
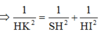
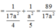
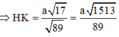
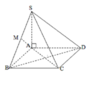
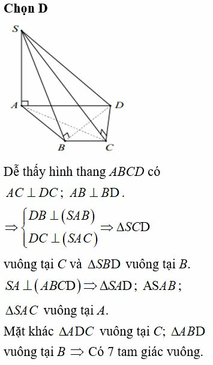
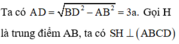
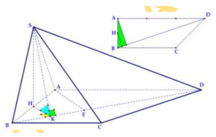
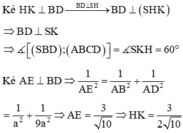



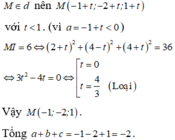



Đáp án là B.
A M ⊥ S B A M ⊥ B C do B C ⊥ S A B ⇒ A M ⊥ S B C .