Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

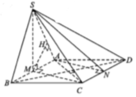
Gọi H là trung điểm của AD. Do tam giác SAD là tam giác đều nên SH vuông góc với AD
Do mặt phẳng (SAD) vuông góc với mặt phẳng (ABCD) nên SH vuông góc với BP(1)
Xét hình vuông ABCD ta có :
\(\Delta CDH=\Delta BCP\Rightarrow CH\perp BP\) (2)
Từ (1) và (2) ta suy ra \(BP\perp\left(SHC\right)\)
Vì \(\begin{cases}MN||SC\\AN||CH\end{cases}\) \(\Rightarrow\left(AMN\right)||\left(SHC\right)\)
\(\Rightarrow BP\perp\left(AMN\right)\Rightarrow BP\perp AM\)
Kẻ vuông góc với mặt phẳng (ABCD), K thuộc vào mặt phẳng (ABCD), ta có :
\(V_{CMNP}=\frac{1}{3}MK.S_{CNP}\)
Vì \(MK=\frac{1}{2}SH=\frac{a\sqrt{3}}{4};S_{CNP}=\frac{1}{2}CN.CP=\frac{a^2}{8}\)
\(\Rightarrow V_{CMNP}=\frac{\sqrt{3}a^2}{96}\)

Lớp 12 thì chúng ta tọa độ hóa cho đơn giản
Gọi O là trung điểm AB \(\Rightarrow SO\perp\left(ABCD\right)\)
\(SO=\dfrac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(AO=BO=\dfrac{a}{2}\)
Đặt hệ trục Oxyz vào chóp, với gốc O trùng O, tia Oz trùng tia OS, tia Ox trùng tia OB, tia Oy trùng tia ON (với N là trung điểm CD). Quy ước \(\dfrac{a}{2}\) là 1 đơn vị độ dài
Ta được tọa độ các điểm: \(S\left(0;0;\sqrt{3}\right)\) ; \(C\left(1;2;0\right)\) ; \(A\left(-1;0;0\right)\) ; \(D\left(-1;2;0\right)\)
Do M là trung điểm SD \(\Rightarrow M\left(-\dfrac{1}{2};1;\dfrac{\sqrt{3}}{2}\right)\)
\(\overrightarrow{AM}=\left(\dfrac{1}{2};1;\dfrac{\sqrt{3}}{2}\right)\) ; \(\overrightarrow{SC}=\left(1;2;-\sqrt{3}\right)\) ; \(\overrightarrow{AC}=\left(2;2;0\right)\)
\(d\left(AM;SC\right)=\dfrac{\left|\left[\overrightarrow{AM};\overrightarrow{SC}\right].\overrightarrow{AC}\right|}{\left|\left[\overrightarrow{AM};\overrightarrow{SC}\right]\right|}=\dfrac{2\sqrt{5}}{5}=\dfrac{a\sqrt{5}}{5}\)

Chọn B.
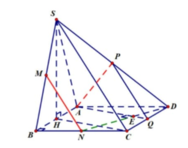
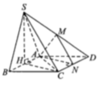
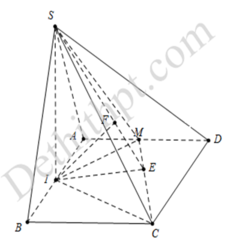
Gọi Q là trung điểm CD, ta có PQ//SC//MN nên MN//(APQ)
=> d(MN, PQ)=d(MN, (APQ))=d(N,(APQ))
Vì N D ⊥ H C N D ⊥ S H ⇒ N D ⊥ ( S H C )
⇒ N D ⊥ S C ⇒ N D ⊥ P Q
A Q → . N D → = ( A D → + D Q → ) . ( D C → + C N → ) = 0 → ⇒ A Q ⊥ N D
Vậy có
N D ⊥ P Q N D ⊥ A Q ⇒ N D ⊥ A P Q t ạ i E ⇒ d ( M N , A P ) = N E
Mà có
1 D E 2 = 1 D A 2 + 1 D Q 2 = 5 a 2 ⇒ D E = a 5
Và D N = a 5 2 ⇒ E N = 3 a 5 10
Vậy d ( M N , A P ) = 2 a 10
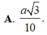
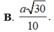

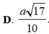
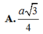
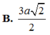
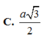
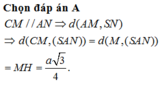



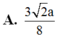
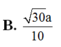
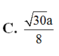
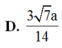
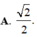
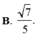
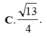
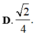

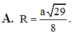
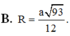
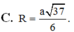
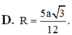
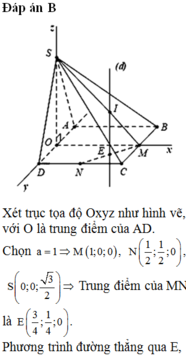

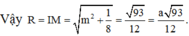
Chọn B