Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

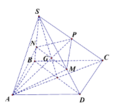
Gọi G là trọng tâm tam giác S A C ⇒ M N đi qua G
V 1 V = 1 2 V S A M N V S A B D + V S M N P V S B D C = 1 2 S M S D . S N S B + S P S C . S M S D . S N S B = 3 4 x . y
V 1 V = 1 2 V S A P N V S A C B + V S A M P V S A D C = 1 2 S P S C . S N S B + S M S D . S P S C = 1 4 x + y
Với x = S N S B ; Y = S M S D
⇒ 3 x y = x + y ≥ 2 x y ⇔ 9 x 2 y 2 ≥ 4 x y ⇔ 3 4 x y ≥ 1 3
Vậy V 1 V đạt giá trị nhỏ nhất bằng 1 3
Đáp án cần chọn là D

Đáp án C.

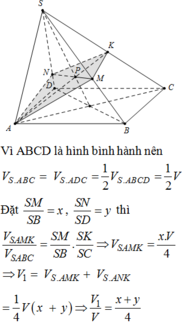
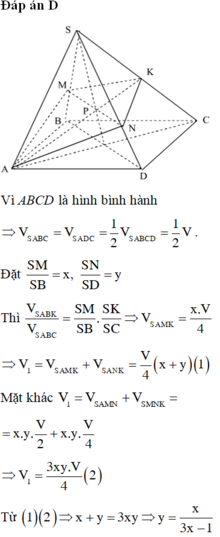
V 1 V = 1 2 V S . A M P V S . A D C + V S . A N P V S . A B C = 1 2 . S P S C S M S D + S N S B = x + y 4 V 1 V = 1 2 V S . A M N V S . A B D + V S . P M N V S . C B D = 1 2 . S M S D + S N S B 1 + S P S C = 3 x y 4 ⇒ x + y = 3 x y ⇒ y = x 3 x − 1 ∈ 0 ; 1 ⇒ x ∈ 1 2 ; 1 ⇒ V 1 V = 3 x 3 4 3 x − 1 = 3 4 f x .
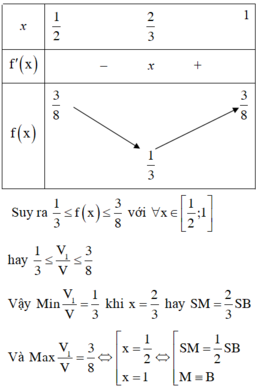
Xét f x = x 2 3 x − 1 với x ∈ 1 2 ; 1
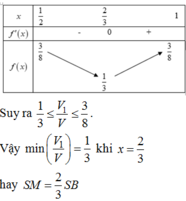
Xét hàm, suy ra M a x 1 2 ; 1 f x = 1 2 ⇒ V 1 V ≤ 3 8 .

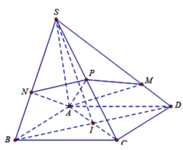
Giả sử S D → = m S M → , S B → = n S N →
Ta có S A → + S C → = S B → + S D → = 2 S I →
Vì A , M , N , P đồng phẳng nên tồn tại các số x;y sao cho A P → = x A M → + y A N →
⇔ 1 2 A S → + A C → = x A S → + S M → + y A S → + S N →
⇔ 1 2 A S → + A S → + S B → + A S → + S D → = x A S → + S M → + y A S → + S N →
⇔ 3 2 A S → + 1 2 S B → + 1 2 S D → = x + y A S → + x m S M → + y n S N →
⇔ x + y = 3 2 x m = 1 2 y n = 1 2 ⇒ m + n = 3.
Ta có: V S . A N P V S . A B C = S N S B . S P S C ⇒ V S . A N P = S N S B . S P S C . V S . A B C = S N S B . 1 2 . V 2 1
V S . A M P V S . A D C = S M S D . S P S C ⇒ V S . A M P = S M S D . S P S C . V S . A D C = S M S D . 1 2 . V 2 2
Từ (1) và (2) V 1 V 2 = 1 4 S B S B + S M S D = 1 4 1 n + 1 m ≥ 1 m + n = 1 3

Đáp án C
Giả sử S D → = m . S M → ; S B → = n . S N → .
S A → + S C → = S B → + S D →
Do A; M; N; K đồng phẳng nên m + n = 3 .
V S . A K M V S . A B C = 1 2 .1. 1 m = 1 2 m ⇒ V S . A K M V = 1 4 m
Tương tự ta có V S . A K N V = 1 4 n ⇒ V ' V = 1 4 . m + n m n = 3 4 m n ≥ 3 m + n 2 = 3 3 2 = 1 3 .
Dấu bằng xảy ra khi m = n = 1,5 .

Đáp án C
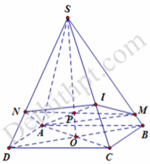
Bài toán sử dụng bổ đề sau: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành. Mặt phẳng (P) bất kì cắt các cạnh SA, SB, SC, SD lần lượt tại các điểm A’, B’, C’, D’ với tỉ số
S A ' S A = x ; S B ' S B = y ; S C ' S C = z ; S D ' S D = t thì ta có đẳng thức
1 x + 1 z = 1 y + 1 t và tỉ số
V S . A ' B ' C ' D ' V S . A B C D = x y z t 4 1 x + 1 y + 1 z + 1 t
Áp dụng vào bài toán
đặt u = S M S B , v = S N S D ta có
1 u + 1 v = S A S A ' + S C S I = 1 1 + 1 2 3 = 5 2 ≥ 2 u v ≥ 16 25 ⇒ V ' V = u v .1. 2 3 4 1 u + 1 v + 1 1 + 1 2 3 = 5 u v 6 ≥ 8 15

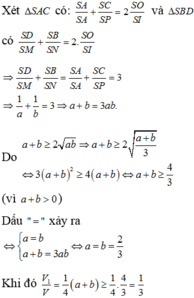
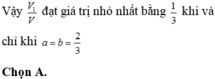
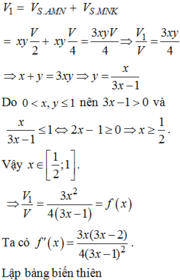
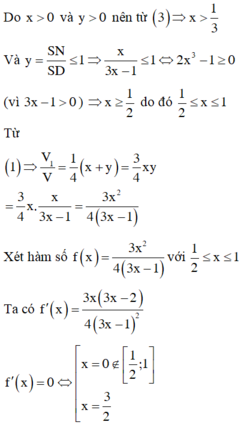
Chọn đáp án B.