Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

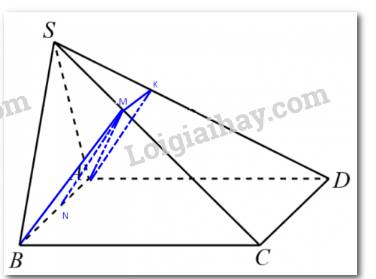
a) Ta có: \(\left( {ABM} \right) \cap \;\left( {ABCD} \right) = AB,\;\left( {ABCD} \right) \cap \;\left( {SCD} \right) = CD,\;AB//CD\).
Suy ra giao tuyến của (ABM) và (SCD) là đường thẳng qua M song song với AB và CD.
Qua M kẻ MK song song với CD (K thuộc SD).
Vậy, K là giao điểm của (AMN) và SD.
Xét tam giác SCD ta có: MK //CD suy ra \(\frac{{SK}}{{SD}} = \frac{{SM}}{{SC}} = \frac{1}{3}\)
b) Xét tam giác SCD ta có: MK //CD suy ra \(\frac{{MK}}{{CD}} = \frac{{SM}}{{SC}} = \frac{1}{3}\)
Lại có \(\frac{{AN}}{{AB}} = \frac{1}{3}\), AB=CD suy ra AN = MK.
Xét tứ giác ANMK ta có: AN = MK, AN // MK suy ra ANMK là hình bình hành.
Do đó MN // AK hay MN // (SAD).

a.
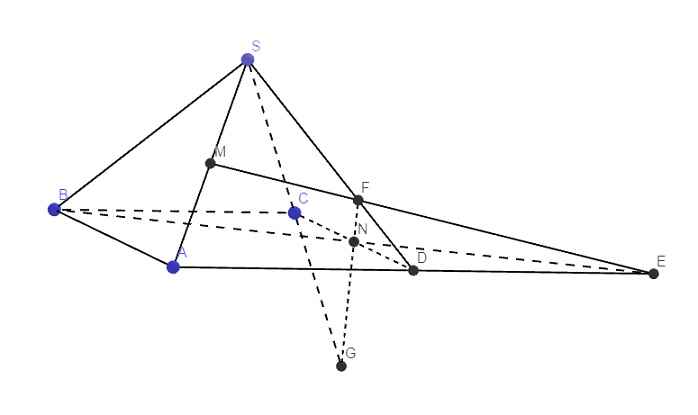
Nối BN kéo dài cắt AD tại E
\(\left\{{}\begin{matrix}E\in\left(BMN\right)\\E\in\left(SAD\right)\end{matrix}\right.\) \(\Rightarrow E=\left(BMN\right)\cap\left(SAD\right)\)
\(\left\{{}\begin{matrix}M\in SA\in\left(SAD\right)\\M\in\left(BMN\right)\end{matrix}\right.\) \(\Rightarrow M=\left(BMN\right)\cap\left(SAD\right)\)
\(\Rightarrow EM=\left(BMN\right)\cap\left(SAD\right)\)
b.
Gọi F là giao điểm EM và SD
Trong mp (SCD), nối FN kéo dài cắt SC kéo dài tại G
\(\Rightarrow G=SC\cap\left(BMN\right)\)

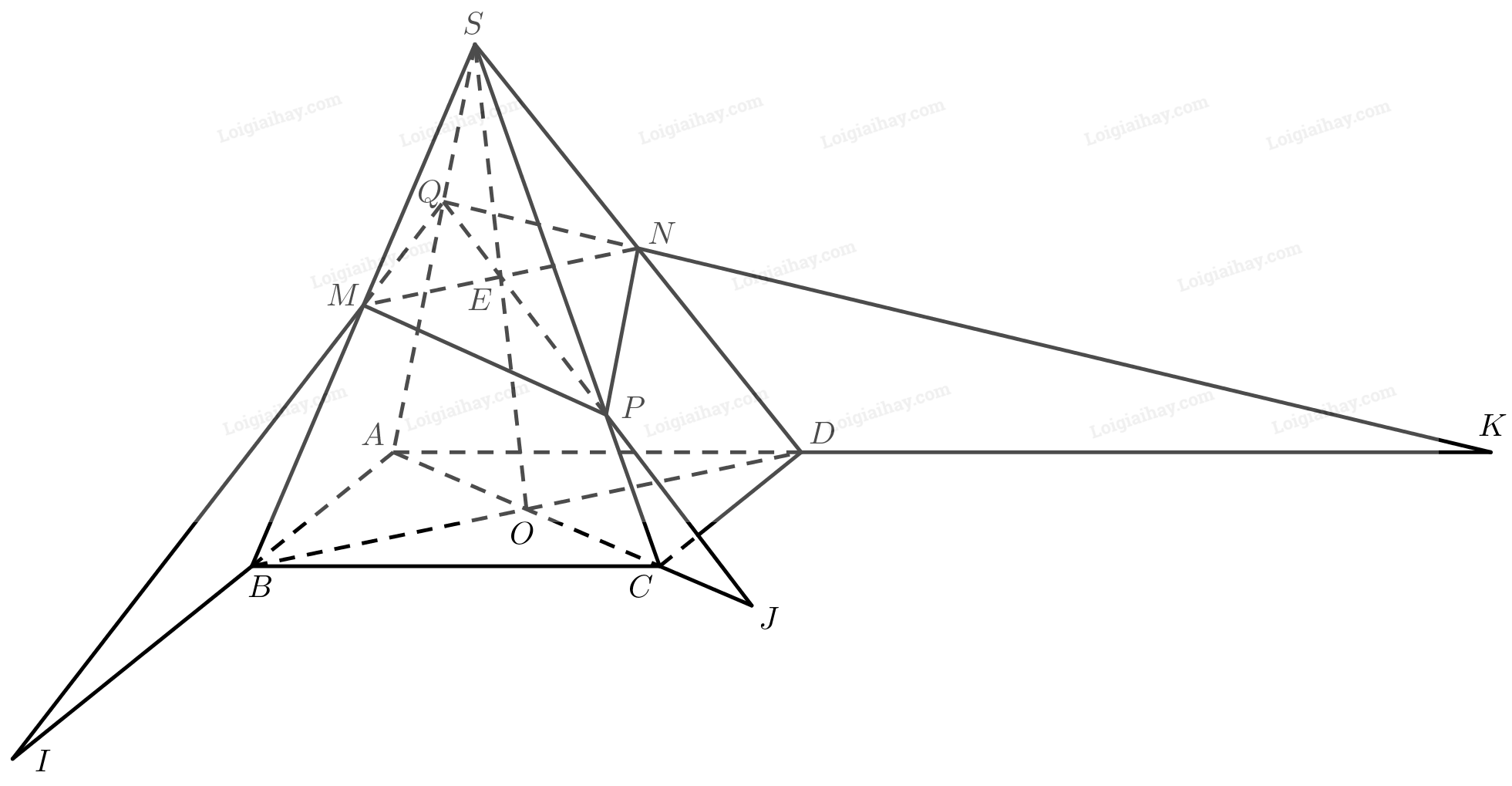
a) Gọi \(E\) là giao điểm của \(SO\) và \(MN\). Ta có:
\(\left. \begin{array}{l}E \in MN \subset \left( {MNP} \right)\\E \in S{\rm{O}}\end{array} \right\} \Rightarrow E = S{\rm{O}} \cap \left( {MNP} \right)\)
b) Gọi \(Q\) là giao điểm của \(SA\) và \(EP\). Ta có:
\(\left. \begin{array}{l}Q \in EP \subset \left( {MNP} \right)\\Q \in S{\rm{A}}\end{array} \right\} \Rightarrow Q = S{\rm{A}} \cap \left( {MNP} \right)\)
c) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in QM \subset \left( {MNP} \right)\\I \in AB \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}J \in QP \subset \left( {MNP} \right)\\J \in AC \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}K \in QN \subset \left( {MNP} \right)\\K \in AD \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow K \in \left( {MNP} \right) \cap \left( {ABCD} \right)\end{array}\)
Do đó, \(I,J,K\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {ABCD} \right)\).
Vậy \(I,J,K\) thẳng hàng.

Qua S kẻ đường thẳng d song song AD (và BC)
Do \(\left\{{}\begin{matrix}S\in\left(SAD\right)\cap\left(SBC\right)\\AD||BC\\AD\in\left(SAD\right)\\BC\in\left(SBC\right)\end{matrix}\right.\) \(\Rightarrow\) giao tuyến của (SAD) và (SBC) là đường thẳng qua S và song song AD, BC
\(\Rightarrow d=\left(SAD\right)\cap\left(SBC\right)\)

a: Xét ΔSBD có
M,N lần lượt là trung điểm của SB,SD
=>MN là đường trung bình
=>MN//BD
BD//MN
\(MN\subset\left(AMN\right)\)
BD không thuộc mp(AMN)
Do đó: BD//(AMN)
b: Gọi O là giao điểm của AC và BD
\(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
Chọn mp(SBD) có chứa MN
(SBD) giao (SAC)=SO(cmt)
Gọi K là giao điểm của SO với MN
=>K là giao điểm của MN với mp(SAC)
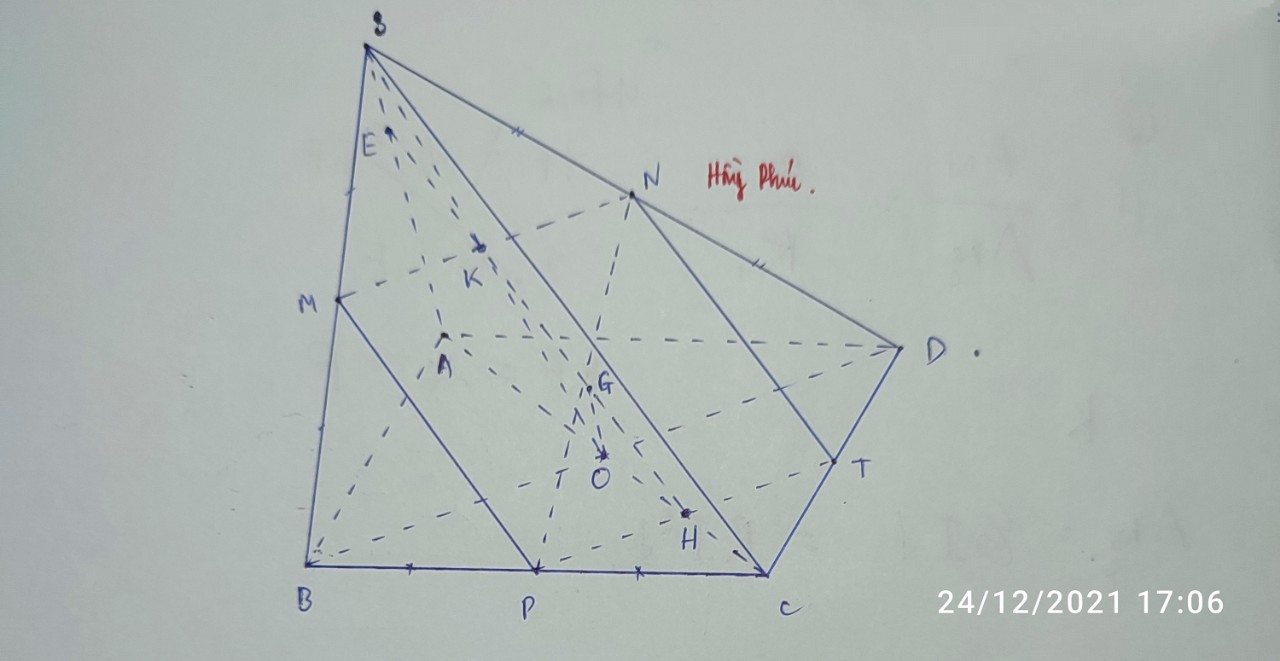
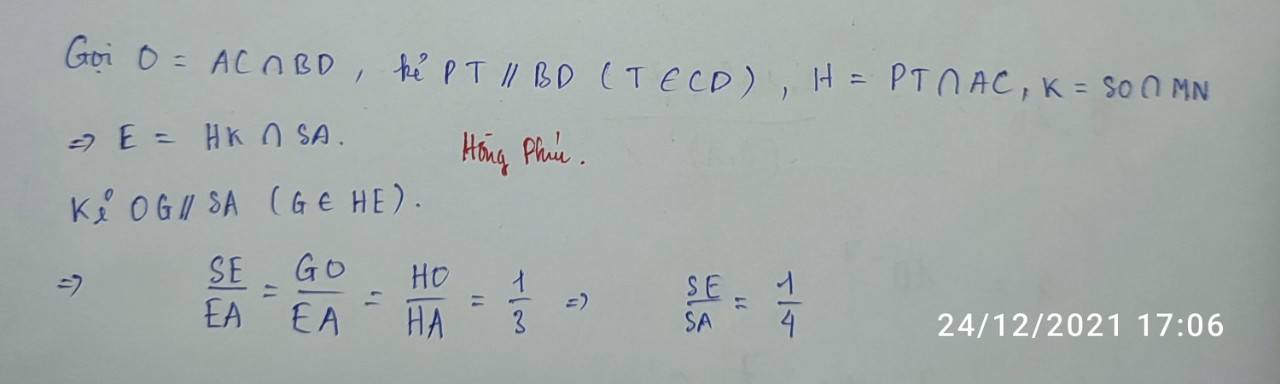
Gọi O là tâm đáy \(\Rightarrow SO=\left(SBD\right)\cap\left(SAC\right)\)
Trong mp (SAC), gọi E là giao điểm SO và MN
MN là đường trung bình tam giác SAC \(\Rightarrow\) E là trung điểm SO
Trong mp (SAD), nối BE kéo dài cắt SD tại K
\(\Rightarrow K=SD\cap\left(BMN\right)\)
Áp dụng định lý Menelaus cho tam giác SOD:
\(\dfrac{ES}{EO}.\dfrac{BO}{BD}.\dfrac{KD}{KS}=1\Rightarrow1.\dfrac{1}{2}.\dfrac{KD}{SK}=1\Rightarrow KD=2SK\)
\(\Rightarrow\dfrac{SK}{SD}=\dfrac{1}{3}\)