Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
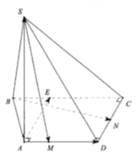
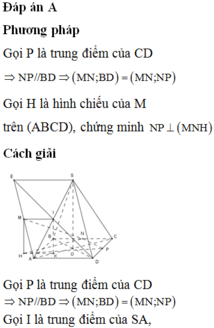
Gọi P là trung điểm của SA. Ta có MNCP là hình bình hành nên MN song song với mặt phẳng (SAC). Mặt khác, BD vuông góc với mặt phẳng (SAC) nên BD vuông góc với MN.
Vì MN song song với mặt phẳng (SAC) nên
\(d\left(MN,AC\right)=d\left(N,SAC\right)\)
\(=\frac{1}{2}d\left(B;\left(SAC\right)\right)=\frac{1}{4}BD=\frac{a\sqrt{2}}{4}\)
Vậy \(d\left(MN;AC\right)=\frac{a\sqrt{2}}{4}\)
Chọn B.
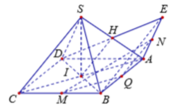
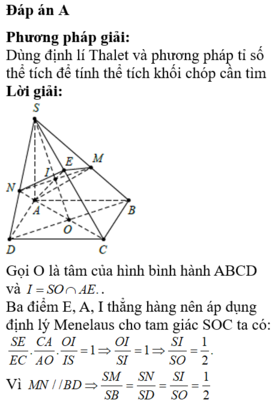
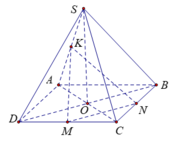
Gọi H = DF ∩ SA => H là trung điểm của ED. I = AC ∩ BD => I là trung điểm BD
Vậy HI là đường trung bình của tam giác BED => HI//EB(1)
Ta có 
(chóp tứ giác đều, hình chiếu của đỉnh S xuống đáy là I)
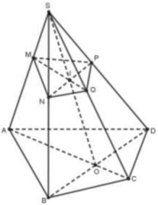
Gọi Q à trung điểm AB; dễ thấy NQ là đường trung bình của tam giác ABE => NQ//BE.
Gọi M là trung điểm BC; dễ thấy MQ//AC , 
Ta có 
Góc giữa hai đường thẳng MN và BD bằng 90 °
Chọn C
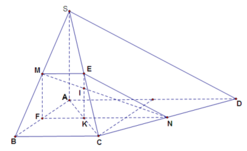
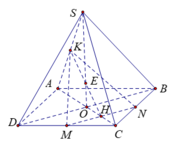
Ta gọi E, F lần lượt là trung điểm của SC, AB
Ta có ME//NF(do cùng song song với BC. Nên tứ giác MENF là hình thang, và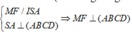 
hay tứ giác MENF là hình thang vuông tại M, F
Ta có: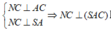 
hay E là hình chiếu vuông góc của N lên (SAC)
Từ đó ta có được, góc giữa MN và (SAC) là góc giữa MN và CI
Suy ra, gọi
α
là góc giữa MN và (SAC) thì 
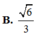
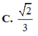
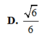
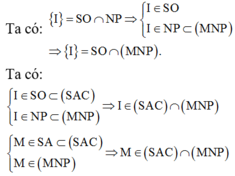
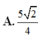
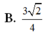
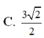
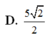
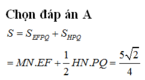
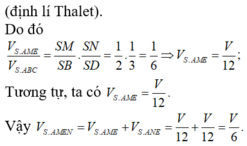
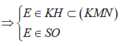
Chọn B