Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
B C D A S E P M N
Gọi P là trung điểm của SA. Ta có MNCP là hình bình hành nên MN song song với mặt phẳng (SAC). Mặt khác, BD vuông góc với mặt phẳng (SAC) nên BD vuông góc với MN.
Vì MN song song với mặt phẳng (SAC) nên
\(d\left(MN,AC\right)=d\left(N,SAC\right)\)
\(=\frac{1}{2}d\left(B;\left(SAC\right)\right)=\frac{1}{4}BD=\frac{a\sqrt{2}}{4}\)
Vậy \(d\left(MN;AC\right)=\frac{a\sqrt{2}}{4}\)
S A B C D M O N H 45 ❤sin45=\(\dfrac{SO}{SM}\) => SO=sin45 . SM= \(\dfrac{\sqrt{2}}{2}.\dfrac{a\sqrt{3}}{2}\) = \(\dfrac{a\sqrt{6}}{4}\)
OM= \(\sqrt{SM^2-SO^2}\) = \(\dfrac{a\sqrt{6}}{4}\)
BC = 2OM => BC=\(\dfrac{a\sqrt{6}}{2}\)
V = \(\dfrac{1}{3}.AB.BC.SO=\dfrac{1}{3}.a.\dfrac{a\sqrt{6}}{2}.\dfrac{a\sqrt{6}}{4}=\dfrac{a^3}{4}\)
❤ta có: SM⊂ (SAB) (1)
mà: \(\left\{{}\begin{matrix}NC//AB\\AB\subset\left(SAB\right)\end{matrix}\right.\) => NC// (SAB) (2)
từ (1) và (2) => SM//NC
\(d_{\left(SM,NC\right)}=d_{\left(NC,\left(SAB\right)\right)}=d_{\left(N,\left(SAB\right)\right)}=2d_{\left(O,\left(SAB\right)\right)}\)
+kẻ OH⊥SM
+ Ta có: \(\left\{{}\begin{matrix}AB\perp OM\\AB\perp SO\end{matrix}\right.\) => AB ⊥ (SOM) \(\supset OH\)
=> \(\left\{{}\begin{matrix}OH\perp AB\\OH\perp SM\end{matrix}\right.\) => OH⊥(SAB)
➜d(O,(SAB)) =OH
OH=\(\dfrac{OM.SO}{\sqrt{OM^2+SO^2}}\)\(\dfrac{a\sqrt{3}}{4}\)
➜d(N,(SAB)) =d(SM,NC)= \(\dfrac{a\sqrt{3}}{2}\)
S B M H A E N C D
Gọi H là hình chiếu vuông góc của S lên AB, suy ra \(SH\perp\left(ABCD\right)\)
Do đó, SH là đường cao của hình chóp S.BMDN
Ta có : \(SA^2+SB^2=a^2+3a^2=AB^2\)
Nên tam giác SAB là tam giác vuông tại S.
Suy ra : \(SM=\frac{AB}{2}=a\) Do đó tam giác SAM là tam giác đều, suy ra \(SH=\frac{a\sqrt{3}}{3}\)
Diện tích của tứ giác BMDN là \(S_{BMDN}=\frac{1}{2}S_{ABCD}=2a^2\)
Thể tích của khối chóp S.BMDN là \(V=\frac{1}{3}SH.S_{BMDN}=\frac{a^3\sqrt{3}}{3}\)
Kẻ ME song song với DN (E thuộc AD)
Suy ra : \(AE=\frac{a}{2}\) Đặt \(\alpha\) là góc giữa 2 đường thẳng SM và DN
Ta có \(\left(\widehat{SM,ME}\right)=\alpha\), theo định lý 3 đường vuông góc ta có \(SA\perp AE\)
Suy ra :
\(SE=\sqrt{SA^2+AE^2}=\frac{a\sqrt{5}}{2};ME=\sqrt{AM^2+AE^2}=\frac{a\sqrt{5}}{2}\)
Tam giác SME là tam giác cân tại E nên \(\begin{cases}\widehat{SME}=\alpha\\\cos\alpha=\frac{\frac{a}{2}}{\frac{a\sqrt{5}}{2}}=\frac{\sqrt{5}}{5}\end{cases}\)
Cho mình hỏi, tam giác cân thì tại sao lại suy ra cos góc kia như thế ??
S A B C D M N H K
Thế tích của khối chóp S.CDNM :
\(S_{CDNM}=S_{ABCD}-S_{AMN}-SBC\)
\(=AB^2-\frac{1}{2}AM.AN-\frac{1}{2}BC.BM\)
\(=a^2-\frac{a^2}{8}-\frac{a^2}{4}=\frac{5a^2}{8}\)
Vậy \(V_{SCDNM}=\frac{1}{3}S_{CDNM.SH}=\frac{5\sqrt{3}a^2}{24}\)
Khoảng cách giữa 2 đường thẳng DM và SC
\(\Delta ADM=\Delta DCN\Rightarrow\widehat{ADM}=\widehat{DCN}\Rightarrow DM\perp CN\)
Kết hợp với điều kiện :
\(DM\perp SH\Rightarrow DM\perp\left(SHC\right)\)
Hạ \(HK\perp SC\left(K\in SC\right)\Rightarrow HK\)là đoạn vuông góc chung của DM và SC
Do đó :
\(d\left(DM,SC\right)=HK\)
Ta có :
\(\begin{cases}HC=\frac{CD^2}{CN}=\frac{2a}{\sqrt{5}}\\HK=\frac{SH.HC}{\sqrt{SH^2+HC^2}}=\frac{2\sqrt{3}a}{\sqrt{19}}\end{cases}\)
\(\Rightarrow d\left(DM,SC\right)=\frac{2\sqrt{3}a}{\sqrt{19}}\)
cậu ơi, hướng dẫn giúp tớ bài tương tự này với: cho hình chóp S.ABCD có ABCD là hình vuông cạnh a, góc giữa SD và mặt phẳng ABCD là 45 độ, SA vuông góc (ABCD). M là trung điểm BC. Tính khoảng cách DM và SC
cảm ơn c nhiều nhiều.
a) Vì I là trọng tâm của tam giác ABD nên \(AI=\dfrac{1}{3}AC\)
S B N M A C O P D
Ta có MN song song với CD và SP vuông góc với CD suy ra MN vuông góc với SP
Gọi O là tâm của đáy ABCD. Ta có :
\(SO=\sqrt{SA^2-OA^2}=\frac{a\sqrt{6}}{2}\)
\(V_{AMNP}=\frac{1}{4}V_{ABSP}=\frac{1}{8}V_{S.ABCD}=\frac{1}{8}.\frac{1}{3}SO.AB^2=\frac{a^2\sqrt{6}}{48}\)
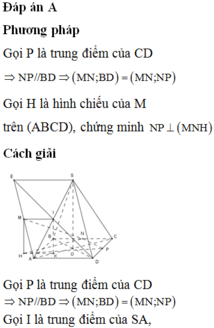
Chọn B.
Gọi H = DF ∩ SA => H là trung điểm của ED. I = AC ∩ BD => I là trung điểm BD
Vậy HI là đường trung bình của tam giác BED => HI//EB(1)
Ta có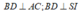
(chóp tứ giác đều, hình chiếu của đỉnh S xuống đáy là I)
Gọi Q à trung điểm AB; dễ thấy NQ là đường trung bình của tam giác ABE => NQ//BE.
Gọi M là trung điểm BC; dễ thấy MQ//AC ,
Ta có
Góc giữa hai đường thẳng MN và BD bằng 90 °