Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án A.
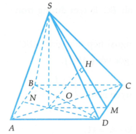
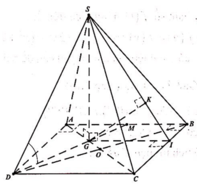
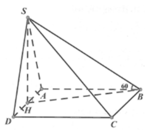
Gọi O là tâm của hình vuông và N là trung điểm của AB.
Khi đó G là giao điểm của AC và DN. Tam giác SGD vuông tại G nên S D G ^ nhọn
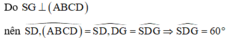
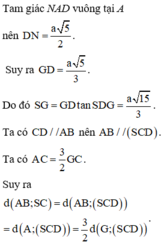


Đáp án A
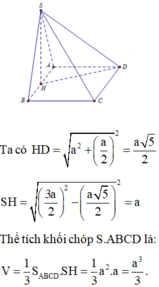
Ta có A D = H A 2 + A D 2 = a 2 2 + a 2 = a 5 2 ⇒ S H = S D 2 - A D 2 = a
Thể tích khối chóp đã cho là: V = 1 3 S H . S A B C D = 1 3 a . a 2 = 1 3 a 3 .

Áp dụng BĐT tam giác ta có:
a+b>c =>c-a<b =>c2-2ac+a2<b2
a+c>b =>b-c <a =>b2-2bc+c2<a2
b+c>a =>a-b<c =>a2-2ab+b2<c2
Suy ra: c2-2ac+a2+b2-2bc+c2+a2-2ab+b2<a2+b2+c2
<=>-2.(ab+bc+ca)+2.(a2+b2+c2)<a2+b2+c2
<=>-2(ab+bc+ca)<-(a2+b2+c2)
<=>2.(ab+bc+ca)<a2+b2+c2

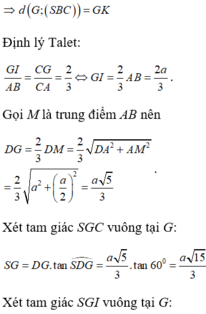
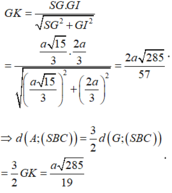




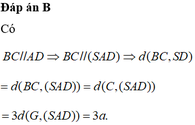
Đáp án C
Phương pháp giải:
Xác định hình chiếu của đỉnh, xác định góc để tìm chiều cao và áp dụng công thức thể tích
Lời giải:
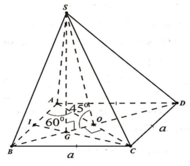
Gọi O là tâm hình vuông ABCD , H là trọng tâm tam giác ABD
Ta có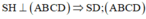
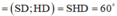
ABCD là hình vuông cạnh a nên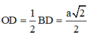
Tam giác HDO vuông tại O, có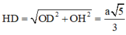
Tam giác SHD vuông tại H, có
Vậy thể tích cần tính là