Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

À, tưởng dài mà thực ra cũng dễ thôi, vì toàn điểm đặc biệt cả.
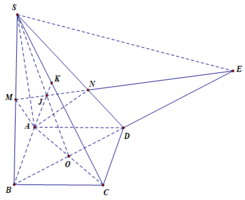
Gọi O là tâm đáy \(\Rightarrow I\) là giao AN và SO
\(\Rightarrow I\) là trọng tâm SAC \(\Rightarrow\dfrac{SI}{SO}=\dfrac{2}{3}\)
Gọi E là giao điểm CM và BD, trong mp (SCM) nối MN cắt SE tại J
E là trọng tâm ABC \(\Rightarrow\dfrac{BE}{BO}=\dfrac{2}{3}\)
Menelaus tam giác BOI:
\(\dfrac{BE}{EO}.\dfrac{OS}{SI}.\dfrac{IJ}{JB}=1\Rightarrow2.\dfrac{3}{2}.\dfrac{IJ}{JB}=1\Rightarrow JB=3IJ\)
\(\Rightarrow IB-IJ=3IJ\Rightarrow\dfrac{IB}{IJ}=4\)

Thưa chị, em không vẽ hình vì sợ duyệt, với lại em lớp 9 nên chỉ làm bài này dựa vào chút kiến thức lớp 8 thôi ạ.
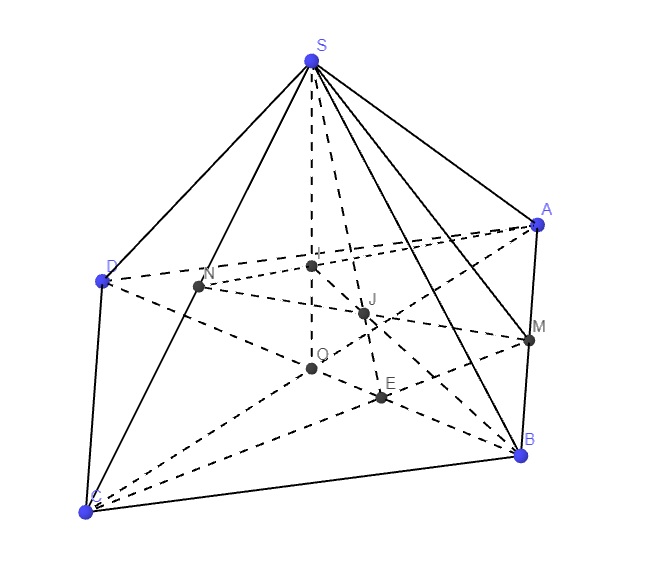
a) Hình bình hành ABCD có O là tâm nên O là trung điểm của đường chéo BD.
Xét \(\Delta BDS\)có I và O lần lượt là trung điểm của BS, BD
\(\Rightarrow\)IO là đường trung bình của \(\Delta BDS\)\(\Rightarrow\)IO//DS
Mà \(DS\in mp\left(SAD\right)\)nên IO//\(mp\left(SAD\right)\)(đpcm)
Em không làm được câu b ạ, em xin lỗi chị.

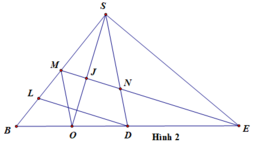


Trong 4 điểm I, J, N, M chỉ có N thuộc CD nên giao điểm của CD và (IJP) là N