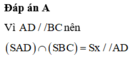Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
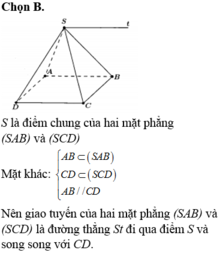
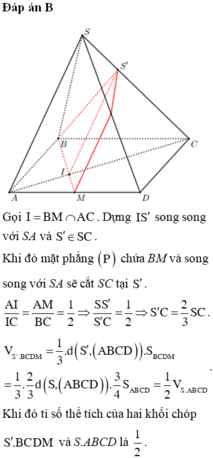
Gọi d là giao tuyến của hai mặt phẳng (SAB) và (SCD).
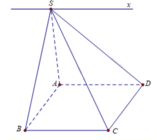
Ba mặt phẳng (SAB),(SCD) và (ABCD) đôi một cắt nhau theo các giao tuyến d; CD; AB. Mà A B / / C D ⇒ d / / A B / / C D ⇒ d là đường thẳng đi qua S và song song với AB và CD =>cố định.
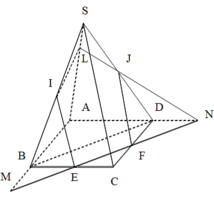
Có I ∈ M Q ⊂ S A B , I ∈ N P ⊂ S C D ⇒ I ∈ d . Vì M là điểm di động trên đoạn AB nên tập hợp các giao điểm I là một đoạn thẳng d. Ta chọn C.

Đáp án D
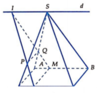
Phương pháp:
Qua M dựng các đường thẳng song song với BD và SC.
Cách giải:

Trong (SAB) kéo dài MN cắt SA tại H.
Vậy thiết diện của chóp khi cắt bởi mặt phẳng (P) là ngũ giác EFPHN.

Chọn A
Xét một trường hợp đặc biệt của các điểm M, E, F ta tính được T = 1.

Đáp án D

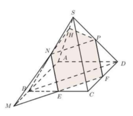
Gọi O là tâm của hình bình hành ABCD, nối S O ∩ A M = I
Qua I kẻ đương thẳng d, song song với BD cắt SB, SD lần lượt tại H, K suy ra S H S B = S K S D = S I S O .
Điểm M ∈ S C thỏa mãn 5 S M = 2 S C ⇒ S M S C = 2 5
Xét tam giác SAC, có:
M S M C . A C A O . I O I S = 1 ⇒ I O S I = 4 3 ⇒ S I S O = 3 7
Khi đó:
V S . A K M V S . A D C = S K S D . S M S C ; V S . A H M V S . A B C = S H S B . S M S C
Suy ra:
V S . A H M K V S . A B C D = S M S C . S H S B = 2 5 . 3 7 = 6 35 ⇒ V S . A H M K = 6 36 V S . A B C D

Đáp án D
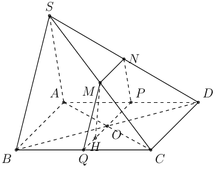
Qua O dựng đường thẳng P Q ∥ A B . Vậy P, Q lần lượt là trung điểm của AD và BC.
Qua P dựng đường thẳng P N ∥ S A . Vậy N là trung điểm của SD
Qua Q dựng đường thẳng Q M ∥ S B . Vậy M là trung điểm của SC.
Nối M và N ⇒ thiết diện của (P) và hình chóp S.ABCD là tứ giác MNPQ.
Vì P Q ∥ C D , M N ∥ C D ⇒ P Q ∥ M N . Vậy tứ giác MNPQ là hình thang.
Ta có P Q = A B = 8 $ , M N = 1 2 A B = 4, M Q = N P = 1 2 S A = 3 . Vậy MNPQ là hình thang cân.
Gọi H là chân đường cao hạ từ đỉnh M của hình thang MNPQ. Khi đó ta có
H Q = 1 4 P Q = 2 ⇒ M H = M Q 2 − H Q 2 = 5
Vậy diện tích của thiết diện cần tìm là S = ( M N + P Q ) M H 2 = 6 5 .

Đáp án D
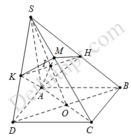
Gọi O là tâm của hình bình hành ABCD, nối S O ∩ A M = I .
Qua I kẻ đường thẳng d, song song với BD cắt SB, SD lần lượt tại H, K suy ra