Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(O\in AC\subset\left(SAC\right)\)
\(O\in BD\subset\left(SBD\right)\)
Do đó: \(O\in\left(SAC\right)\cap\left(SBD\right)\)
mà \(S\in\left(SAC\right)\cap\left(SBD\right)\)
nên \(\left(SAC\right)\cap\left(SBD\right)=SO\)
\(D\in FS\subset\left(SFE\right)\)
\(B\in SE\subset\left(SFE\right)\)
Do đó: \(BD\subset\left(SFE\right)\)
Ta có: \(O\in BD\subset\left(SEF\right)\)
\(O\in AC\subset\left(ACD\right)\)
Do đó: \(O\in\left(SEF\right)\cap\left(ACD\right)\)
mà \(D\in\left(SEF\right)\cap\left(ACD\right)\)
nên \(\left(SEF\right)\cap\left(ACD\right)=DO\)
b: Xét ΔSDB có
E,F lần lượt là trung điểm của SB,SD
=>EF là đường trung bình của ΔSDB
=>EF//DB
Xét (ABCD) và (AEF) có
BD//EF
\(A\in\left(ABCD\right)\cap\left(AEF\right)\)
Do đó: (ABCD) giao (AEF)=xy, xy đi qua A và xy//BD//EF

Chọn đáp án C
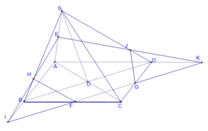
Trong mp (ABCD), gọi

Do đó ngũ giác EHFGJ là thiết diện của hình chóp cắt bởi (EFG)

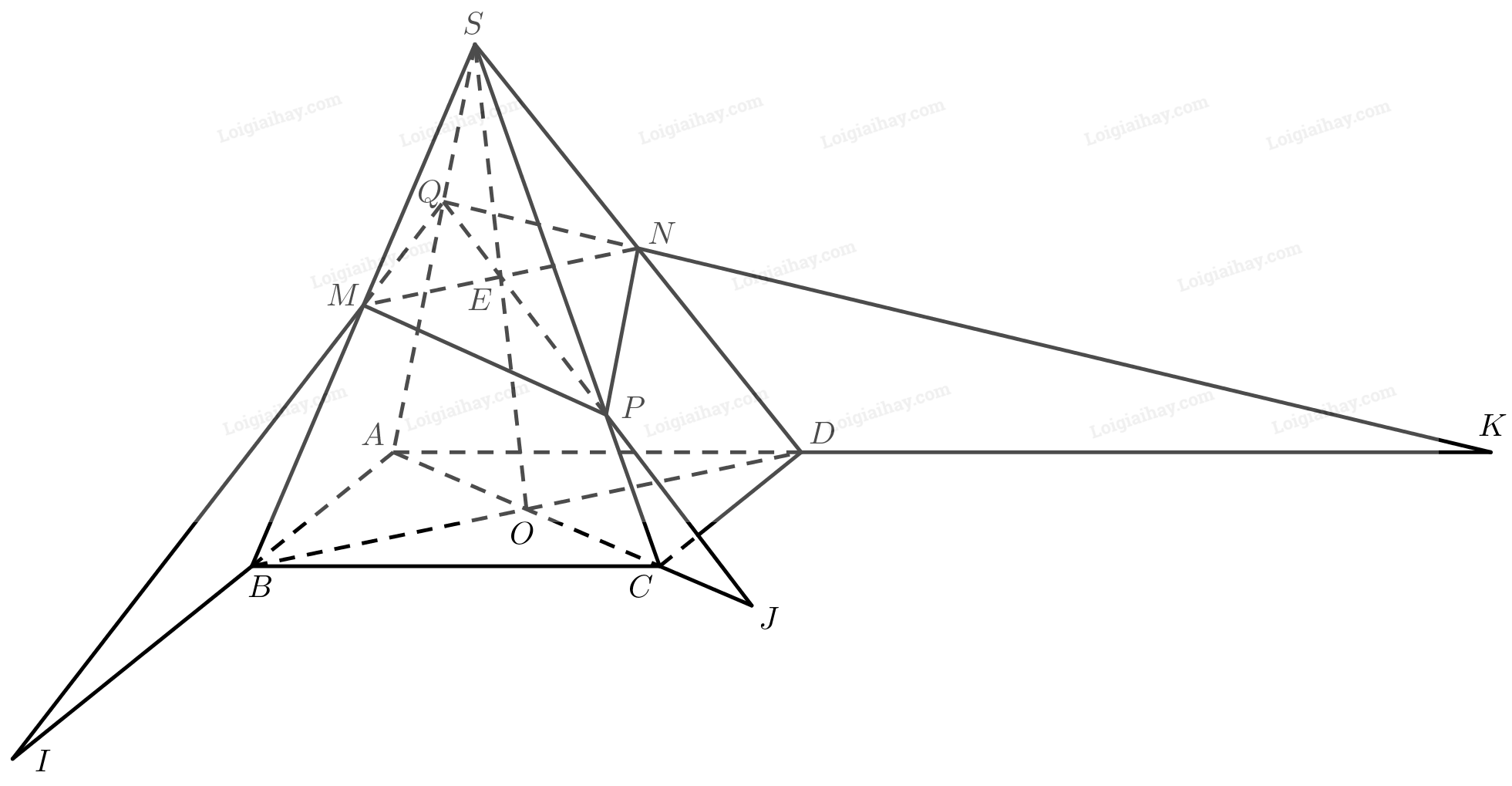
a) Gọi \(E\) là giao điểm của \(SO\) và \(MN\). Ta có:
\(\left. \begin{array}{l}E \in MN \subset \left( {MNP} \right)\\E \in S{\rm{O}}\end{array} \right\} \Rightarrow E = S{\rm{O}} \cap \left( {MNP} \right)\)
b) Gọi \(Q\) là giao điểm của \(SA\) và \(EP\). Ta có:
\(\left. \begin{array}{l}Q \in EP \subset \left( {MNP} \right)\\Q \in S{\rm{A}}\end{array} \right\} \Rightarrow Q = S{\rm{A}} \cap \left( {MNP} \right)\)
c) Ta có:
\(\begin{array}{l}\left. \begin{array}{l}I \in QM \subset \left( {MNP} \right)\\I \in AB \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow I \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}J \in QP \subset \left( {MNP} \right)\\J \in AC \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {MNP} \right) \cap \left( {ABCD} \right)\\\left. \begin{array}{l}K \in QN \subset \left( {MNP} \right)\\K \in AD \subset \left( {ABC{\rm{D}}} \right)\end{array} \right\} \Rightarrow K \in \left( {MNP} \right) \cap \left( {ABCD} \right)\end{array}\)
Do đó, \(I,J,K\) cùng nằm trên giao tuyến của hai mặt phẳng \(\left( {MNP} \right)\) và \(\left( {ABCD} \right)\).
Vậy \(I,J,K\) thẳng hàng.

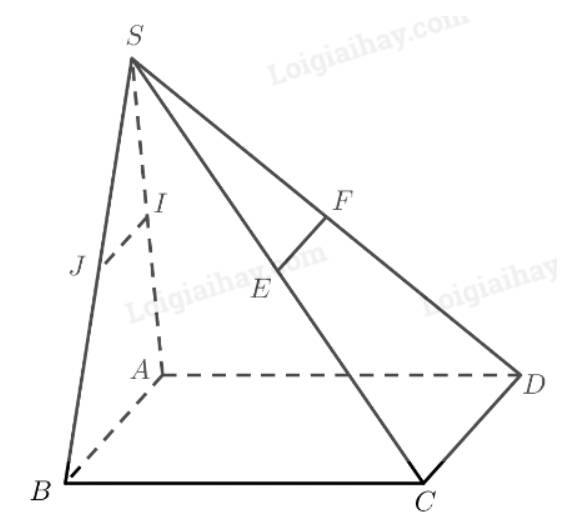
Ta có: \(I\) là trung điểm của \(SA\)
\(J\) là trung điểm của \(SB\)
\( \Rightarrow IJ\) là đường trung bình của tam giác \(SAB\)
\( \Rightarrow IJ\parallel AB\)
\(E\) là trung điểm của \(SC\)
\(F\) là trung điểm của \(SD\)
\( \Rightarrow EF\) là đường trung bình của tam giác \(SC{\rm{D}}\)
\( \Rightarrow EF\parallel C{\rm{D}}\)
Mà \(AB\parallel C{\rm{D}}\).
Vậy \(IJ\parallel EF\parallel AB\parallel C{\rm{D}}\).
Vậy \(AD\) không song song với \(IJ\)
Chọn C.

a) Để tìm giao điểm M của SD và (GHK), ta có thể sử dụng tính chất của đường thẳng và mặt phẳng. Đầu tiên, ta cần tìm phương trình đường thẳng SD và phương trình mặt phẳng GHK. Sau đó, ta giải hệ phương trình để tìm giao điểm M.
b) Để chứng minh G, E, M thẳng hàng, ta có thể sử dụng định lý về trọng tâm của tam giác và tính chất của trung điểm. Chúng ta cần chứng minh rằng G, E, M nằm trên cùng một đường thẳng.

Chọn C.
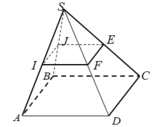
+) Ta có, IJ là đường trung bình tam giác SAB nên IJ // AB. ⇒ D đúng.
+) ABCD là hình bình hành nên AB// CD. Mà IJ// AB
Suy ra , IJ // CD ⇒ B đúng.
+) EF là đường trung bình tam giác SCD nên EF // CD.
Suy ra, IJ // EF ⇒ A. đúng.
- Do đó chọn đáp án C.
b) Trong (SCD): Gọi M là giao của GF và CD.
Trong (SBD): Gọi N là giao của EG và BD.
Trong (ABCD): Gọi H là giao của AC và MN.
Vậy H là giao của đường thẳng AC và (EFG).