T
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
22 tháng 9 2023
Tham khảo:
a) Gọi E là giao điểm của AB và CD
Vì AB thuộc mp (SAB) nên E là giao điểm của CD và (SAB)
b) Ta có: S thuộc hai mặt phẳng (SAB) và (SCD)
E thuộc hai mặt phẳng (SAB) và (SCD)
Suy ra SE là giao tuyến của hai mặt phẳng (SAB) và (SCD)
c) Trong mp (SAB), gọi G là giao điểm của ME và SB
Mà SB thuộc (SBC), ME thuộc (MCD)
Do đó: G thuộc hai mặt phẳng (MCD) và (SBC)
C thuộc hai mặt phẳng (MCD) và (SBC)
Suy ra CG là giao tuyến của hai mặt phẳng (MCD) và (SBC).
QT
Quoc Tran Anh Le
Giáo viên
23 tháng 8 2023
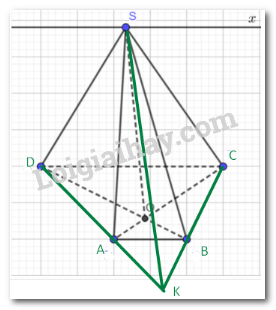
a) Gọi giao điểm của AD và BC là K.
Ta có: SK cùng thuộc mp(SAD) và (SBC).
Vậy SK là giao tuyến của (SAD) và (DBC).
b) (SAB) và (SCD) có AB // CD và S chung nên giao tuyến là dường thẳng Sx đi qua x và song song với AB và CD.
c) Gọi O là giao điểm của AC và BD suy ra O thuộc giao tuyến của (SAC) và (SBC)
Suy ra SO là giao tuyến của (SAC) và (SBD).
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 8 2023
- Ta có: AB thuộc (SAB)
CD thuộc (SCD)
Mà AB // CD, S là điểm chung của hai mặt phẳng (SAB) và (SCD).
Từ S kẻ Sx sao cho Sx // AB // CD.
Vậy Sx là giao tuyến của hai mặt phẳng (SAB) và (SCD).
- Tương tự ta có: Sy là giao tuyến của hai mặt phẳng (SAD) và (SBC) sao cho Sy // AD // BC.
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 12 2020
Kéo dài AB và CD cắt nhau tại E
\(\Rightarrow SE=\left(SAB\right)\cap\left(SCD\right)\)
Qua M kẻ đường thẳng d song song CD lần lượt cắt AC và AD tại F và G
Trong mp (SAC), qua F kẻ đường thẳng song song SA cắt SC tại P
Trong mp (SAD), qua G kẻ đường thẳng song song SA cắt SD tại Q
\(\Rightarrow\) Hình thang MPQG là thiết diện của (P) và chóp
28 tháng 8 2023
2:
a: AD và BC là hai đường thẳng song song
b: \(S\in\left(SAB\right)\)
\(S\in\left(SCD\right)\)
Do đó:S là giao điểm của hai mặt phẳng (SAB) và (SCD)
c: AB//CD
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
Do đó; \(\left(SAB\right)\cap\left(SCD\right)=mn\), mn đi qua S và mn//AB//CD
31 tháng 3 2023
a: (SBD) giao (ABCD)=BD
SO vuông góc BD
AO vuông góc BD
=>((SBD);(ABCD))=góc SOA
b: (SCD) giao (SAD)=SD
Kẻ AH vuông góc SC
ΔSDC vuông tại D
Kẻ DK vuông góc SC
Qua H kẻ HF//DK
=>Góc cần tìm là góc AHF
28 tháng 10 2023
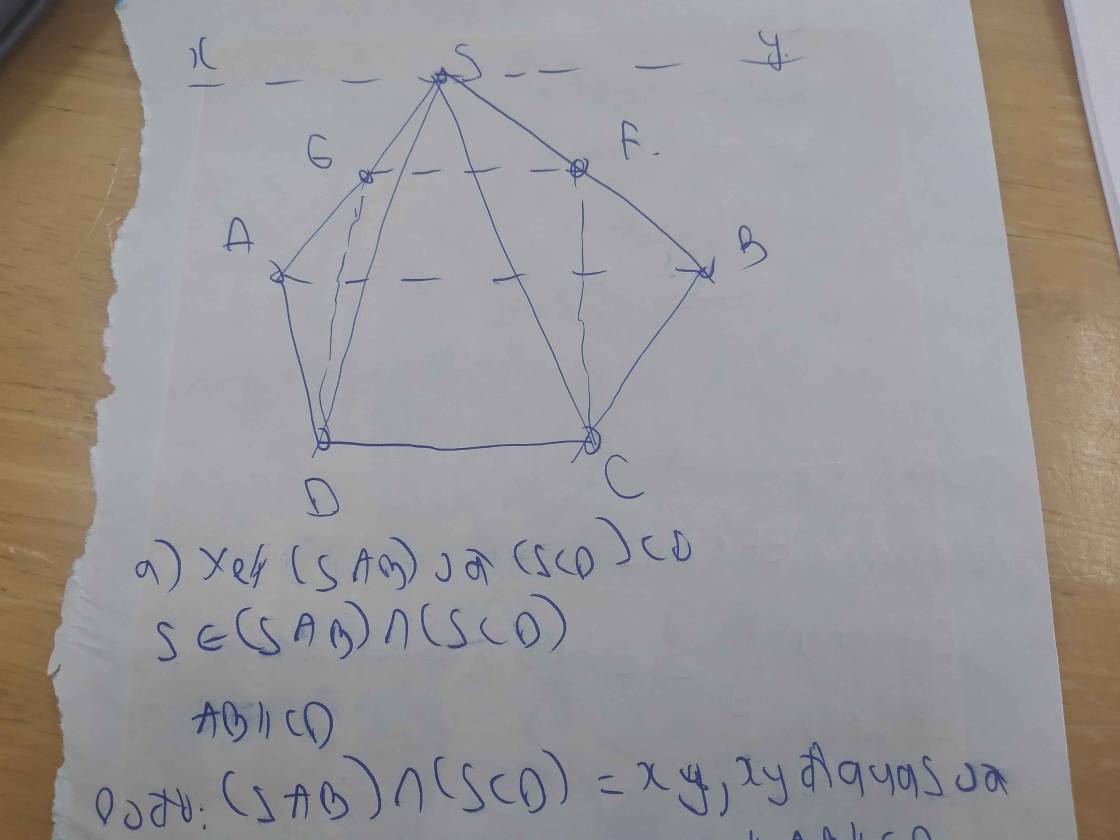
a: Xét (SAB) và (SCD) có
\(S\in\left(SAB\right)\cap\left(SCD\right)\)
AB//CD
Do đó: (SAB) giao (SCD)=xy, xy đi qua S và xy//AB//CD
Xét (SAD) và (SBC) có
\(S\in\left(SAD\right)\cap\left(SBC\right)\)
AD//BC
Do đó: (SAD) giao (SBC)=mn, mn đi qua S và mn//AD//BC
c: \(N\in SB\subset\left(SAB\right);N\in\left(NCD\right)\)
=>\(N\in\left(SAB\right)\cap\left(NCD\right)\)
Xét (SAB) và (NCD) có
\(N\in\left(SAB\right)\cap\left(NCD\right)\)
AB//CD
Do đó: (SAB) giao (NCD)=ab, ab đi qua N và ab//CD//AB
31 tháng 3 2023
a: Qua S kẻ đường Sx song song SD
=>Sx vuông góc SA
SC vuông góc CD
=>SC vuông góc Sx
((SAB);(SCD))=góc ASC
b: (SBD) căt (SAB)=SB
Kẻ DA vuông góc AB
mà DA vuông góc SA
nên DA vuông góc (SAB)
=>DA vuông góc SB
Kẻ AK vuông góc SB
=>((SBD);(SAB))=góc AKD
c: (SBC) giao (SCD)=SC
Kẻ BH vuông góc SC
Qua H kẻ HF//CD
=>HF vuông góc SC
=>((SBC);(SCD))=góc BHF
Gọi E là giao điểm của AB và CD
\(E\in AB\subset\left(SAB\right);E\in CD\subset\left(SCD\right)\)
Do đó: \(E\in\left(SAB\right)\cap\left(SCD\right)\)
mà \(S\in\left(SAB\right)\cap\left(SDC\right)\)
nên \(\left(SAB\right)\cap\left(SCD\right)=SE\)