Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Từ giả thiết ta có SO là trục của đường tròn ngoại tiếp tam giác ABC và SA=SB=a. Trong mặt phẳng (SAO), trung trực của cạnh SA cắt SO tại I thì I là tâm của mặt cầu ngoại tiếp hình chóp. Khi đó ta tính được:
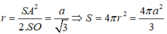

Giả sử (O,R) là tâm đường tròn ngoại tiếp tg ABC
=> A'O _|_(ABC)
=> V(ABC.A'B'C') = A'O.S(ABC)
*S(ABC) = (AB.AC.sin120)/2 = 4a^2
Lại có ^A'AO = 30o là góc tạo bở cạnh bên và mặt đáy
=> A'O = OA.tan 30 = R.√3/3
Mặt khác áp dụng định lý sin tg ABC
=> AB/sin ^BCA =2R
=> R = AB/2sin^BCA = 4a
=> A'O = 4a√3/3
=> V(ABC.A'B'C') = 4a√3/3. 4a^2 = (16√3a^3)/3
* Giả sử OA cắt BC tại M
Do tg ABC cân => AM _|_BC, mà BC _|_A'O
=> BC _|_(A'OM) -----------(*)
Từ M kẻ MN _|_AA' , Do (*) => BC _|_MN
=> MN là đường vuông góc chung AA' và BC
Do A'AO = 30 => MN = AM.sin 30 = AM/2
mà AM = AB.sin^ABC = AB.sin30 = AB/2 = 2a
=> MN =a

Đáp án B
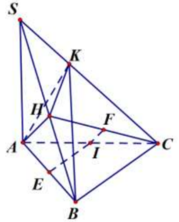
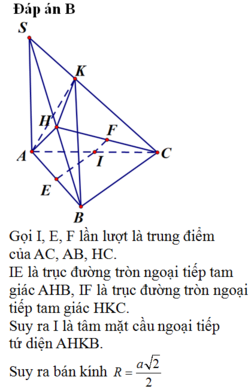
Gọi I, E, F lần lượt là trung điểm của AC, AB, HC. IE là trục đường tròn ngoại tiếp tam giác AHB, IF là trục đường tròn ngoại tiếp tam giác HKC.
⇒ IA=IB=IC=IH=IK
Suy ra I là tâm mặt cầu ngoại tiếp tứ diện AHKB.
Suy ra bán kính R= a 2 2
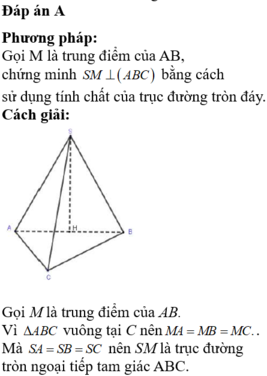

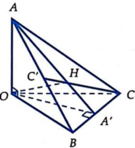


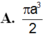
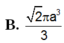

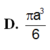
Đáp án C
* Hướng dẫn giải:
Hình chop S.ABC thoả mãn SA = SB = SC do đó S thuộc trục đường tròn ngoại tiếp tam giác ABC
Chân đường cao hạ từ S là tâm đường tròn ngoại tiếp tam giác đáy
dễ thấy H là tâm đường tròn ngoại tiếp tam giác ABC