

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




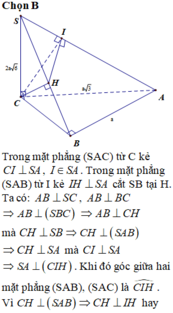
Qua C kẻ đường thẳng vuông góc AC cắt AB kéo dài tại D
\(\left\{{}\begin{matrix}SC\perp\left(ABC\right)\Rightarrow SC\perp CD\\CD\perp AC\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAC\right)\)
Kẻ \(CH\perp SB\Rightarrow CH\perp\left(SAB\right)\)
\(\Rightarrow\widehat{HCD}\) là góc giữa (SAB) và (SAC)
\(BC=\sqrt{AC^2-AB^2}=a\sqrt{2}\)
\(\dfrac{1}{CH^2}=\dfrac{1}{SC^2}+\dfrac{1}{BC^2}=\dfrac{13}{24a^2}\Rightarrow CH=\dfrac{2a\sqrt{78}}{13}\)
\(CD=AC.tanA=AC.\dfrac{BC}{AB}=a\sqrt{6}\)
\(sin\widehat{HCD}=\dfrac{DH}{CD}=\dfrac{\sqrt{CD^2-CH^2}}{CD}=...\)

Chọn đáp án B
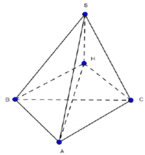
Gọi là H hình chiếu của đỉnh S xuống mặt phẳng (ABC). Khi đó, ta có
![]()
Ta có
![]()
Tương tự, ta cũng chứng minh được
![]()
Từ đó suy ra
![]()
Do SH ⊥ AB, BH ⊥ AB nên suy ra góc giữa (SAB) và (ABC) là góc SBH. Vậy SBH = 60 0
![]()
Trong tam giác vuông ABH, ta có
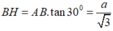
Trong tam giác vuông SHB, ta có
![]()

Chọn A

Gọi H là trung điểm của AC. Đỉnh S cách đều các điểm A, B, C
=> SH ⊥ (ABC)
Xác đinh được
![]()
Ta có MH // SA
![]()
Gọi I là trung điểm của AB => HI ⊥ AB
![]()
và chứng minh được HK ⊥ (SAB)
![]()
Trong tam giác vuông SHI tính được
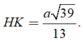

Chọn D.
Lời giải.
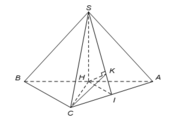
Ta có
![]()
![]()
![]()
Từ (1) và (2)
![]()
Gọi I là trung điểm AC
![]()
Mặt khác
![]()
Từ (3) và (4)
![]()
![]()
![]()
![]()
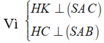
nên góc giữa hai mặt phẳng (SAC) và (SAB) bằng góc giữa hai đường thẳng HK và HC.
Xét tam giác CHK vuông tại K, có
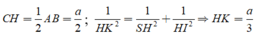
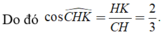

Kẻ \(BK\perp AC\Rightarrow BK\perp\left(SAC\right)\)
\(\Rightarrow BK=d\left(B;\left(SAC\right)\right)\)
\(\dfrac{1}{BK^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow BK=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{a\sqrt{3}}{2}\)
Kẻ \(CP\perp BH\Rightarrow CP\perp\left(SBH\right)\)
\(\Rightarrow CP=d\left(C;\left(SBH\right)\right)\)
\(\widehat{CBP}=\widehat{ACB}=30^0\Rightarrow CH=BC.sin30^0=\dfrac{a\sqrt{3}}{2}\)
\(BH=\dfrac{AC}{2}=\dfrac{1}{2}\sqrt{AB^2+AC^2}=a\)\(\Rightarrow SH=\sqrt{SB^2-BH^2}=a\)
Kẻ \(HE\perp BC\) , kẻ \(HF\perp SE\Rightarrow HF=d\left(H;\left(SBC\right)\right)\)
\(HE=CH.sin30^0=\dfrac{a}{2}\)
\(\dfrac{1}{HF^2}=\dfrac{1}{SH^2}+\dfrac{1}{HE^2}\Rightarrow HF=\dfrac{SH.HE}{\sqrt{SH^2+HE^2}}=\dfrac{a\sqrt{5}}{5}\)