Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a.
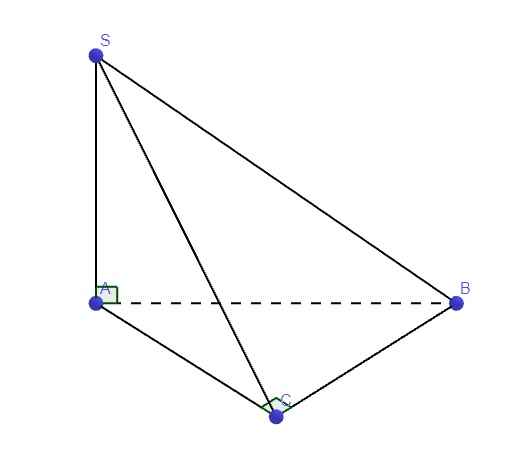
Do \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AB\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAB\right)\)
\(\Rightarrow BC\perp SB\)
b.
\(SA\perp\left(ABC\right)\Rightarrow AC\) là hình chiếu vuông góc của SC lên (ABC)
\(\Rightarrow\widehat{SCA}\) là góc giữa SC và (ABC)
\(AC=\sqrt{AB^2+BC^2}=a\sqrt{2}\)
\(\Rightarrow tan\widehat{SCA}=\dfrac{SA}{AC}=1\Rightarrow\widehat{SCA}=45^0\)

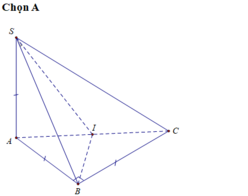
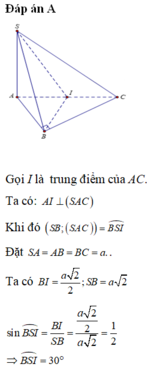
Gọi M là trung điểm AC \(\Rightarrow BM\perp AC\)
\(\Rightarrow BM\perp\left(SAC\right)\Rightarrow\widehat{BSM}\) là góc giữa SB và (SAC)
\(AC=a\sqrt{2}\) ; \(AM=BM=\dfrac{AC}{2}=\dfrac{a\sqrt{2}}{2}\)
\(SA=\sqrt{SC^2-AC^2}=a\Rightarrow SB=a\sqrt{2}\)
\(sin\widehat{BSM}=\dfrac{BM}{SB}=\dfrac{1}{2}\Rightarrow\widehat{BSM}=30^0\)

a: (SB;(ABC))=(BS;BA)=góc SBA
BA^2+BC^2=AC^2
=>2*BA^2=AC^2
=>AB=BC=a
tan SBA=SA/SB=căn 3
=>góc SBA=60 độ
d: (SB;(BAC))=(BS;BA)=góc SBA=60 độ
e:
CB vuông góc AB
CB vuông góc SA
=>CB vuông góc (SBA)
=>(SC;(SBA))=(SC;SB)=góc BSC
SB=căn SA^2+AB^2=2a
SC=căn SA^2+AC^2=a*căn 5
Vì SB^2+BC^2=SC^2
nên ΔSBC vuông tại B
sin BSC=BC/SC=a/a*căn 5=1/căn 5
=>góc BSC\(\simeq27^0\)

Chọn D
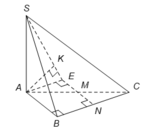
Xác định được
![]()
![]()
Gọi N là trung điểm BC, suy ra MN//AB.
Lấy điểm E đối xứng với N qua M, suy ra ABNE là hình chữ nhật.
Do đó
![]()
![]()

a: \(\widehat{SB;AB}=\widehat{SBA}\)
SA\(\perp\)(ABC)
=>\(SA\perp AB;SA\perp AC;SA\perp BC\)
Xét ΔSAB vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
=>\(\widehat{SBA}=60^0\)
=>\(\widehat{SB;AB}=60^0\)
b:
\(\widehat{SC;AC}=\widehat{SCA}\)
Xét ΔSAC vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
nên \(\widehat{SCA}=60^0\)
=>\(\widehat{SC;AC}=60^0\)
c: ΔABC đều có AM là đường trung tuyến
nên \(AM=BC\cdot\dfrac{\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{2}\)
Ta có: SA\(\perp\)(ABC)
AM\(\subset\)(ABC)
Do đó: SA\(\perp\)AM
=>ΔSAM vuông tại A
\(\widehat{SM;AM}=\widehat{SMA}\)
Xét ΔSMA vuông tại A có \(tanSMA=\dfrac{SA}{AM}=\dfrac{a\sqrt{3}}{\dfrac{a\sqrt{3}}{2}}=2\)
=>\(\widehat{SMA}\simeq63^026'\)
=>\(\widehat{SM;AM}\simeq63^026'\)
a.
Góc giữa SB và AB là góc \(\widehat{SBA}\)
Trong tam giác vuông SAB:
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\dfrac{a\sqrt{3}}{a}=\sqrt{3}\)
\(\Rightarrow\widehat{SBA}=60^0\)
b.
Góc giữa SC và AC là góc \(\widehat{SCA}\)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)
c.
Góc giữa SM và AM là góc \(\widehat{SMA}\)
AM là trung tuyến tam giác đều \(\Rightarrow AM=\dfrac{a\sqrt{3}}{2}\)
\(\Rightarrow tan\widehat{SMA}=\dfrac{AM}{SA}=2\Rightarrow\widehat{SMA}=60^026'\)

Do SA ⊥ (ABCD) ⇒ \(\left\{{}\begin{matrix}SA\perp AB\\SA\perp AC\\SA\perp BC\end{matrix}\right.\)
Mà BC ⊥ AC ⇒ BC ⊥ (SAC) ⇒ BC ⊥ SC và BC ⊥ AH
Do BC ⊥ AH và AH ⊥ SC ⇒ AH ⊥ (SBC) ⇒ AH ⊥ KH ⇒ \(\widehat{AHK}=90^0\)
ΔSAB và ΔSAC vuông tại A
Mà AH và AK lần lượt là đường cao của ΔSAB và ΔSAC
⇒ \(\left\{{}\begin{matrix}SA^2=SK.SB\\SA^2=SH.SC\end{matrix}\right.\)
⇒ SK . SB = SH . SC
⇒ \(\dfrac{SK}{SH}=\dfrac{SC}{SB}\) ⇒ ΔSKH \(\sim\) ΔSCB ⇒ \(\widehat{SKH}=\widehat{SCB}=90^0\)
⇒ HK ⊥ SB
Mà AK⊥ SB
⇒ ((SAB),(SCB)) = (AK,AH) = \(\widehat{KAH}\) = 450 (đây là góc nhọn, vì \(\widehat{AHK}=90^0\))
⇒ ΔHAK vuông cân tại H ⇒ AK = \(\sqrt{2}AH\)
Ta có : \(\dfrac{S_{SAC}}{S_{SAB}}=\dfrac{\dfrac{1}{2}.AH.SC}{\dfrac{1}{2}AK.SB}=\dfrac{\dfrac{1}{2}.SA.AC}{\dfrac{1}{2}.SA.AB}\)
⇒ \(\dfrac{AH.SC}{AK.SB}=\dfrac{SA.AC}{SA.AB}\)
⇒ \(\dfrac{1}{\sqrt{2}}\) . \(\dfrac{SC}{SB}\) = \(\dfrac{AC}{AB}\). Mà AC = a và AB = 2a
⇒ \(\dfrac{1}{\sqrt{2}}\)\(\dfrac{SC}{SB}\) = \(\dfrac{1}{2}\) ⇒ \(\dfrac{SC^2}{SB^2}\) = \(\dfrac{1}{2}\) . Mà SB2 - SC2 = BC2 = 3a2
⇒ \(\left\{{}\begin{matrix}SC^2=3a^2\\SB^2=6a^2\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}SB=a\sqrt{6}\\SC=a\sqrt{3}\end{matrix}\right.\) ⇒ SA = a\(\sqrt{2}\)
Từ đó ta tính được SH = \(\dfrac{2a\sqrt{3}}{3}\) và SK = \(\dfrac{a\sqrt{6}}{3}\)
Gọi M là trung điểm của SB thì ta có CM // HK (cùng vuông góc với SB)
Khoảng cách từ HK đến AC bằng khoảng cách từ HK đến (AMC)

\(SA\perp\left(ABC\right)\Rightarrow AB\) là hình chiếu vuông góc của SB lên (ABC)
\(\Rightarrow\widehat{SBA}\) là góc giữa SB và (ABC)
\(AB=AC\sqrt{2}=a\sqrt{2}\)
\(tan\widehat{SBA}=\dfrac{SA}{AB}=\sqrt{\dfrac{3}{2}}\Rightarrow\widehat{SBA}\approx50^046'\)
\(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\Rightarrow SA\perp BC\\AC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SAC\right)\)
\(\Rightarrow SC\) là hình chiếu vuông góc của SB lên (SAC)
\(\Rightarrow\widehat{BSC}\) là góc giữa SB và (SAC)
\(SB=\sqrt{SA^2+AB^2}=a\sqrt{5}\) ; \(BC=AC=a\)
\(sin\widehat{BSC}=\dfrac{BC}{SB}=\dfrac{1}{\sqrt{5}}\Rightarrow\widehat{BSC}\approx26^034'\)
b.
Theo cmt, \(BC\perp\left(SAC\right)\)
Mà \(BC=\left(SBC\right)\cap\left(ABC\right)\)
\(\Rightarrow\widehat{SCA}\) là góc giữa (SBC) và (ABC)
\(tan\widehat{SCA}=\dfrac{SA}{AC}=\sqrt{3}\Rightarrow\widehat{SCA}=60^0\)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABC\right)\\SA\in\left(SAC\right)\end{matrix}\right.\) \(\Rightarrow\left(SAC\right)\perp\left(ABC\right)\)
\(\Rightarrow\) Góc giữa (SAC) và (ABC) là 90 độ

a: ΔACB vuông tại C
=>\(CA^2+CB^2=AB^2\)
=>\(AB=\sqrt{\left(3a\right)^2+\left(4a\right)^2}=5a\)
\(\widehat{SB;\left(ABC\right)}=\widehat{BS;BA}=\widehat{SBA}\)
Xét ΔSBA vuông tại A có \(tanSBA=\dfrac{SA}{AB}=\dfrac{5a}{5a}=1\)
nên \(\widehat{SBA}=45^0\)
=>\(\widehat{SB;\left(ABC\right)}=45^0\)
b: \(\widehat{SC;\left(ABC\right)}=\widehat{CS;CA}=\widehat{SCA}\)
Xét ΔSCA vuông tại A có \(tanSCA=\dfrac{SA}{AC}=\dfrac{5}{3}\)
nên \(\widehat{SCA}\simeq59^0\)
=>\(\widehat{SC;\left(ABC\right)}\simeq59^0\)
c: Ta có: BC\(\perp\)AC
BC\(\perp\)SA
AC,SA cùng thuộc mp(SAC)
Do đó:BC\(\perp\)(SAC)
=>BC\(\perp\)SC tại C
\(\widehat{SB;\left(SAC\right)}=\widehat{SB;SC}=\widehat{BSC}\)
Ta có: ΔSAC vuông tại A
=>\(SA^2+AC^2=SC^2\)
=>\(SC=\sqrt{\left(5a\right)^2+\left(3a\right)^2}=a\sqrt{34}\)
Xét ΔSCB vuông tại C có \(tanBSC=\dfrac{BC}{SC}=\dfrac{4a}{a\sqrt{34}}=\dfrac{4}{\sqrt{34}}\)
nên \(\widehat{BSC}\simeq34^026'\)
=>\(\widehat{SB;\left(SAC\right)}\simeq34^026'\)