Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

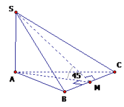
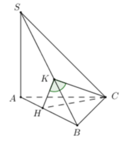
1) Gọi H là trung điểm của AB.
ΔSAB đều → SH ⊥ AB
mà (SAB) ⊥ (ABCD) → SH⊥ (ABCD)
Vậy H là chân đường cao của khối chóp.

a) Tính \(V_{S.ABM}\)
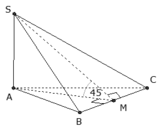
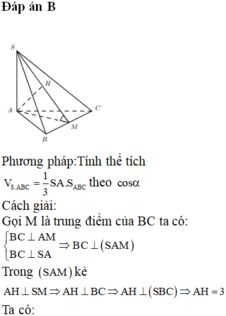
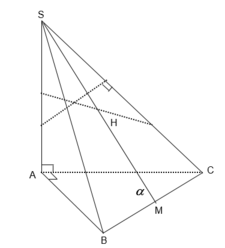
Tam giác ABC cân tại A , SBC cân tại S \(\Rightarrow AM\perp BC;SM\perp BC\) tại M
Vì mp(SBC) vuông góc với mặt đáy suy ra SM vuông góc với mặt đáy
Góc giữa SB và mặt đáy là góc SBM=300
\(\Rightarrow SM=BMtan.\widehat{SBM}=\frac{a}{2}.tan30^0=\frac{a}{2\sqrt{3}}\)
\(\Rightarrow V_{S.ABM}=\frac{1}{3}.SM.S_{ABM}=\frac{1}{3}.\frac{a}{2\sqrt{3}}.\frac{1}{2}.\frac{a}{2}.\frac{a\sqrt{3}}{2}=\frac{a^3}{48}\)
b) Tính k/c SB và AM
Kẻ MH vuông góc với SB tại H
Dễ dàng chứng minh MH là đoạn vuông góc chung giữa SB và AM
Vậy khảong cách giữa SB và AM bằng đoạn MH và bằng \(\frac{BM}{cos.\widehat{HBM}}=\frac{\frac{a}{2}}{cos30^0}=\frac{a}{\sqrt{3}}\)

Hai mặt phẳng (SAB) và (SAC) cùng vuông góc với (ABC) \(\Rightarrow SA\perp\left(ABC\right)\)
\(AB\perp BC\Rightarrow SB\perp BC\Rightarrow\widehat{SBA}\) là góc giữa 2 mặt phẳng (SBC) và mặt phẳng (ABC)
\(\Rightarrow\widehat{SBA}=60^o\)
\(\Rightarrow SA=AB.\tan\widehat{SBA}=2a\sqrt{3}\)
Mặt phẳng qua SM và song song với BC, cắt AC tại N
\(\Rightarrow MN||BC\) và N là trung điểm của \(AC\\ \)
\(MN=\frac{BC}{2}=a;BM=\frac{AB}{2}=a\)
Diện tích \(S_{BCNM}=\frac{\left(BC+MN\right).BM}{2}=\frac{3a^2}{2}\)
Thể tích \(V_{S.BCNM}=\frac{1}{3}S_{BCNM}.SA=a^3\sqrt{3}\)
Kẻ đường thẳng \(\Delta\) đi qua N, song song với AB
Hạ \(AD\perp\Delta\left(D\in\Delta\right)\Rightarrow AB||\left(SND\right)\)
\(\Rightarrow d\left(AB;SN\right)=d\left(AB,\left(SND\right)\right)=d\left(A,\left(SND\right)\right)\)
Hạ \(AH\perp SD\left(H\in SD\right)\Rightarrow AH\perp\left(SND\right)\Rightarrow d\left(A,\left(SND\right)\right)=AH\)
Tam giác SAD vuông tại A : \(\begin{cases}AH\perp SD\\AD=MN=a\end{cases}\)
\(\Rightarrow d\left(AB,SN\right)=AH=\frac{SA.AD}{\sqrt{SA^2+AD^2}}=\frac{2a\sqrt{39}}{13}\)

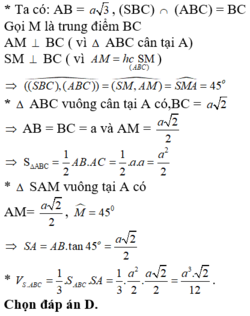
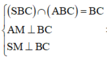
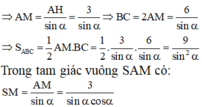
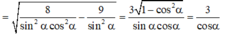
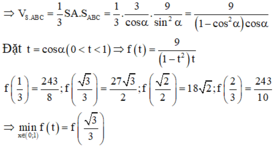
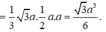



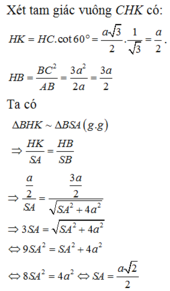
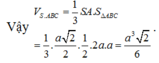
S A B C M
Ta có : \(SA\perp BC\), \(AB\perp BC\) \(\Rightarrow SB\perp BC\)
Do đó : góc giữa 2 mặt phẳng (SBC) và (ABC) bằng \(\widehat{SBA}=30^0\)
\(V_{S.ABM}=\frac{1}{2}V_{S.ABC}=\frac{1}{2}SA.AB.BC\)
\(BC=AB=a;SA=AB.\tan30^0=\frac{a\sqrt{3}}{3}\)
Vậy \(V_{s.ABM}=\frac{a^3\sqrt{3}}{36}\)