Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

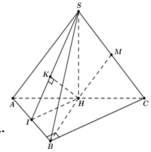
Gọi H là trung điểm của AC
Đỉnh S cách đều các điểm A, B, C ![]()
Xác đinh được ![]()
Ta có MH//SA ![]()
Gọi I là trung điểm của AB ![]()
![]() và chứng minh được
và chứng minh được ![]()
Trong tam giác vuông SHI tính được ![]()
Chọn A.

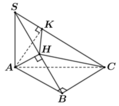
Theo giả thiết, ta có ![]() và
và ![]()
Do 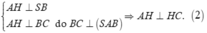
Từ (1) và (2) suy ra ba điểm B, H, K cùng nhìn xuống AC dưới một góc 90 ° nên
Chọn C.

Chọn B.
Phương pháp:
+ Gọi H là trung điểm BC. Ta chứng minh A H ⊥ A B C và AH là trục đường tròn ngoại tiếp tam giác
SBC
+ Suy ra tâm mặt cầu ngoại tiếp chóp S. ABC là giao của AH và đường trung trực cạnh AB.
+ Chỉ ra tam giác SBC vuông tại S từ đó tính SC theo định lý Pytago.
Cách giải:




Đáp án C

Gọi O = A C ∩ B D , G = A O ∩ A C '
Ta có A C ⊥ ( S B D ) mặt khác S C ⊥ B ' D ' ⇒ B ' D ' ⊥ ( S A C ) ⇒ B ' D ' / / B D
Theo Định lý Talet ta có S B ' B ' B = S D ' D ' D = S G G O = 2 ⇒ G là trọng tâm ∆ S A C ⇒ C ' là trung điểm SC
Vậy V S A B ' C ' D ' V S A B C D = V S A B ' C ' + V S A C ' D ' V S A B C D = 1 2 ( V S A B ' C ' V S A B C + V S A C ' D ' V S A C D ) = 1 2 S B ' . S C ' S B . S C + S C ' . S D ' S C . S D
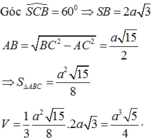
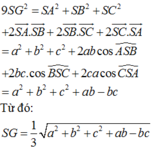
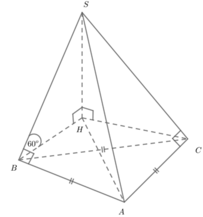


Đáp án B
Gọi D là hình chiếu của S trên (ABC). Khi đó S D ⊥ A B C .
Do đó hình chiếu của SC trên (ABC) là CD. Suy ra góc giữa SC và (ABC) là S C D ^ .
Ta có B C ⊥ S C B C ⊥ S D ⇒ B C ⊥ C D , A B ⊥ S A A B ⊥ S D ⇒ A B ⊥ A D .
Vậy ABCD là hình chữ nhật.
Theo đề S C D ^ = 60 0 . Ta tính được B D = A C = a 5 , D S = C D 3 = a 3 .
Vậy S B = S D 2 + B D 2 = 8 a 2 = 2 a 2 .