
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



BC và AK cắt BC tại H.Ta có HB=HC (AK là trung trực của BC)
=>HC=BC/2.
AH=√(AC²-CH²);
∆ACH~∆COH (tam giác vuông chung góc nhọn tại O)
=>AH/AC=HC/CO=>CO=AC.HC/AH.
=20.12/√(20²-12²)=20.12/16=15.
Gọi AH, BK là hai đường cao, có AH = 10; BK = 12
thấy hai tgiác CAH và CBK đồng dạng => CA/AH = CB/BK
=> CA/10= 2CH/12 => CA = 2,6.CH (1)
mặt khác áp dụng pitago cho tgiac vuông HAC:
CA² = CH² + AH² (2)
thay (1) vào (2): 2,6².CH² = CH² + 102
=> (2,6² - 1)CH² = 102=> CH = 10 /2,4 = 6,5
=> BC = 2CH = 13 cm

Chọn C.
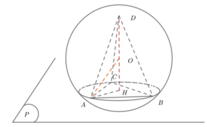
Phương pháp: Tìm vị trí điểm D để thể tích ABCD lớn nhất.
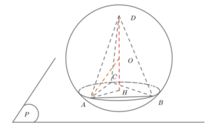

Đáp án là B
Gọi O 1 ; O 2 ; O 3 lần lượt là tâm của 3 mặt cầu và A ,B,C lần lượt là hình chiếu của 3 tâm trên mặt phẳng đã cho.
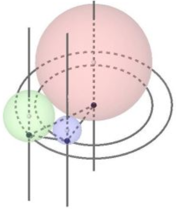
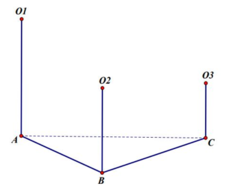

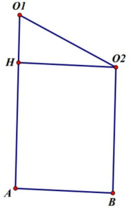
Suy ra:
A H = R 2 ; O 1 H = R 1 − R 2 ; O 2 H = A B ;
O 1 O 2 = R 1 + R 2
Xét tam giác vuông O 1 O 2 H: O 1 O 2 2 = O 1 H 2 + A B 2
⇒ R 1 + R 2 2 = R 1 − R 2 2 + A B 2
⇒ R 1 . R 2 = A B 2 4
Tương tự: R 2 . R 3 = B C 2 4 ; R 1 . R 3 = A C 2 4 ⇒ R 1 . R 2 . R 3 = 3