Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

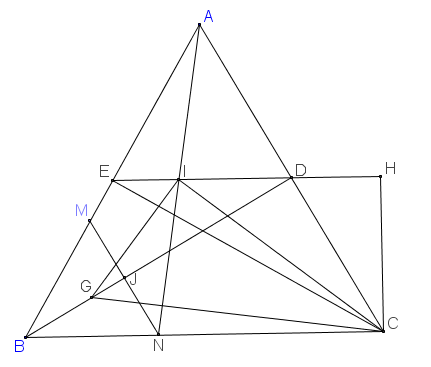
Gọi E là trung điểm của MB, P là giao điểm của AI với CD. Đặt AB = a
Theo định lý Ta-lét. Ta có: \(\frac{1}{2}=\frac{GE}{GN}=\frac{AE}{NP}\)
A M E G B I P C N D
\(=\frac{\frac{2}{3}AB}{\frac{1}{2}CD+CP}=\frac{4a}{3a+6CP}\Rightarrow CP=\frac{5a}{6}\)
Suy ra \(\frac{IB}{IC}=\frac{AB}{CP}=\frac{6}{5}\)
Vì \(\frac{GA}{GP}=\frac{GE}{GM}=\frac{1}{2}\)nên \(\frac{GA}{AP}=\frac{1}{3}\) (1)
Mà \(\frac{IA}{IP}=\frac{IB}{IC}=\frac{6}{5}\)nên kết hợp với (1) ta được: \(\frac{GI}{AP}=\frac{AI}{AP}-\frac{AG}{AP}=\frac{6}{11}-\frac{1}{3}=\frac{7}{33}\) (2)
Chia theo vế của (1) cho (2) ta được:
\(\frac{GA}{GI}=\frac{11}{7}\)
Tóm lại \(\frac{GA}{GI}=\frac{11}{7};\frac{IB}{IC}=\frac{6}{5}\)

Một đội xe tải trong 3 ngày phải chuyển hết một số hàng hóa 2 ngày đầu độc chất thải đã chuyển được 13,14 số hàng hóa biết rằng ngày thứ hai đội chuyển được 3/7 số hàng hóa vận chuyển ít hơn ngày thứ nhất 30 tấn hỏi ngày thứ ba đôi chân bao nhiêu hàng hóa
Gọi E, D lần lượt là trung điểm AB, AC, ta có I, E, D thẳng hàng
MN cắt BD tại J, hạ CH vuông góc ED tại H
Có DH=DC2=ED2DH=DC2=ED2
=>EDEH=23EDEH=23
Có BGBD=BGBJ.BJBDBGBD=BGBJ.BJBD
=23.BNBC=EDEH.EIED=23.BNBC=EDEH.EIED
=>BGBD=EIEHBGBD=EIEH
<=>BGEI=BDEHBGEI=BDEH (1)
Ta có △CBD∼△CEH△CBD∼△CEH (g, g)
=>CBCE=BDEH=BGEICBCE=BDEH=BGEI
=>△CBG∼△CEI△CBG∼△CEI (c, g, c) (2)
(2) =>ˆBCG=ˆECIBCG^=ECI^
<=>ˆBCG+ˆGCE=ˆGCE+ˆECIBCG^+GCE^=GCE^+ECI^
<=>ˆBCE=ˆGCIBCE^=GCI^ (3)
(2) =>BCEC=GCICBCEC=GCIC (4)
từ (3, 4) =>△BEC∼△GIC△BEC∼△GIC (c, g, c)
=>ˆI=90∘I^=90∘, ˆG=60∘G^=60∘ (đpcm)
Hình gửi kèm

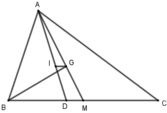
Gọi D, M là giao điểm của AI, AG với BC.
Vì AD là tia phân giác góc B A C ^ nên B D A B = D C A C (t/c)
⇒ B D 12 = D C 18 = B D + D C 12 + 18 = 15 30 = 1 2
=> BD = 12. 1 2 = 6, DC =18. 1 2 = 9
Lại có: BI là tia phân giác A B D ^ nên A I I D = A B B D = 12 6 = 2 (tính chất)
=> I D A D = M G M A = 1 3 hay D đúng
Mà AG = 2GM (vì G là trọng tâm)
Nên A I I D = A G G M = 2 hay B đúng
Theo định lí đảo của định lí Talet ta có:
IG // DM => IG // BC hay A đúng
Chỉ có C sai
Đáp án: C