Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì AE=CF và AE//CF (AB//CD do hbh ABCD) nên AECF là hbh
\(\left\{{}\begin{matrix}AE=CF\\AM=CN\\\widehat{A}=\widehat{C}\left(hbh.ABCD\right)\end{matrix}\right.\Rightarrow\Delta AME=\Delta CNF\left(c.g.c\right)\\ \Rightarrow ME=NF\left(4\right)\\ \left\{{}\begin{matrix}AE=CF\\AB=CD\end{matrix}\right.\Rightarrow AB-AE=CD-CF\Rightarrow BE=DF\left(1\right)\\ \left\{{}\begin{matrix}AM=CN\\AD=BC\end{matrix}\right.\Rightarrow AD-AM=CN-BC\Rightarrow DM=BN\left(2\right)\)
ABCD là hbh nên \(\widehat{B}=\widehat{D}\left(3\right)\)
\(\left(1\right)\left(2\right)\left(3\right)\Rightarrow\Delta DMN=\Delta BFE\left(c.g.c\right)\\ \Rightarrow MN=EF\left(5\right)\)
(4)(5) suy ra MENF là hbh

A B C D E F M N O
Gọi O là giao điểm 2 đường chéo AC và BD
Xét \(\Delta\)AOE và \(\Delta\)COF có:AO=OC ( vì ABCD là hình bình hành ),CF=AE ( giả thiết ),^AOE=^COF ( đối đỉnh )
a
Vì vậy \(\Delta AOE=\Delta COF\left(c.g.c\right)\Rightarrow OE=OF\left(1\right)\)
Xét \(\Delta\)BON và \(\Delta\)DOM có:OB=OD ( vì ABCD là hình bình hành ),MD=BN ( vì AM=CN ),^MOD=^NOB ( đối đỉnh )
Vì vậy \(\Delta BON=\Delta COM\left(c.g.c\right)\Rightarrow OM=ON\left(2\right)\)
Từ \(\left(1\right);\left(2\right)\) suy ra tứ giác EMFN là hình bình hành.
b
Hình bình hành EMFN có O là giao điểm của 2 đường chéo,tứ giác ABCD có O là giao điểm của 2 đường chéo.
=> ĐPCM
P/S:Mik ko chắc lắm đâu nha,nhất là câu b ý:p

em gửi bài qua fb thầy chữa cho nhé, tìm fb của thầy bằng sđt: 0975705122 nhé.

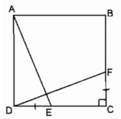
Xét ∆ ADE và ∆ DCF:
AD = DC (gt)
∠ A = ∠ D = 90 °
DE = CF (gt)
Do đó: ∆ ADE = ∆ DCF (c.g.c)
⇒ AE = DF
∠ (EAD) = ∠ (FDC)
∠ (EAD) + ∠ (DEA) = 90 ° (vì ΔADE vuông tại A)
⇒ ∠ (FDC) + ∠ (DEA) = 90 °
Gọi I là giao điểm của AE và DF.
Suy ra: ∠ (IDE) + ∠ (DEI) = 90 °
Trong ∆ DEI ta có: ∠ (DIE) = 180 ° – ( ∠ (IDE) + ∠ (DEI) ) = 180 ° – 90 ° = 90 °
Suy ra: AE ⊥ DF

S_EFGH = S_ABCD - S_BGF - S_GCH - S_AEHD
Là các hình tam giác vuông và hình thang vuông, dễ dàng tìm được hàm diện tích của EFGH theo x: -2x2 + 32.5x
Nếu được thì đạo hàm là tìm được giá trị x mà S max.
Đề bài yêu cầu gì?