Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

làm đc mỗi câu b :))
AEFC là hình bình hành ( tự cm nhá :) )
=> đường chéo AC giao đường chéo EF tại trung điểm của EF
câu a => đường chéo MN giao đường chéo EF tại trung điểm của EF
=> ĐPCM
câu b thui, câu a lằng nhằng quá lười nghĩ thông cảm nhé

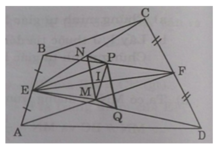
a) Xét tam giác ABF có:
E là trung điểm của AB
P là trung điểm của BF
⇒ EP là đường trung bình của ΔABF
⇒ EP // AF và EP = AF/2
M là trung điểm AF (gt)
⇒ MF = AF/2
Do đó EP // MF và EP = MF. Vậy EPFM là hình bình hành
I là giao điểm của hai đường chéo MP và EF nên I là trung điểm của MP.
b) Do tứ giác EPFM là hình bình hành nên I là trung điểm của EF.
Chứng minh tương tự ta có ENFQ là hình bình hành mà I là trung điểm của EF ⇒ I là trung điểm của NQ (2)
Từ (1) và (2) ⇒ MNPQ là hình bình hành (hai đường chéo cắt nhau tại trung điểm mỗi đường).

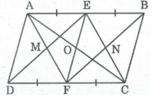
Gọi O là giao điểm của AC và EF
Tứ giác AECF là hình bình hành ⇒ OE = OF
Tứ giác EMFN là hình bình hành nên hai đường chéo cắt nhau tại trung điểm của mỗi đường.
Suy ra: MN đi qua trung điểm O của EF.
Vậy AC, EF, MN đồng quy tại O.


a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
Xét tứ giác AEFD có
AE//FD
AE=FD
Do đó: AEFD là hình bình hành
Xét tứ giác BEFC có
BE//FC
BE=FC
Do đó: BEFC là hình bình hành
Xét tứ giác BEDF có
BE//DF
BE=DF
Do đó: BEDF là hình bình hành
b: Ta có:ABCD là hình bình hành
nên AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Ta có: BEDF là hình bình hành
nên BD cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của BD
nên O là trung điểm của FE
hay F,O,E thẳng hàng