Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

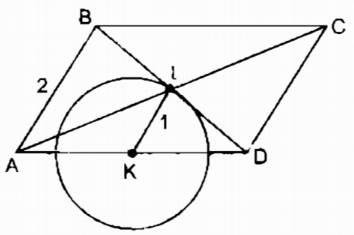
Gọi K là trung điểm của cạnh AD.
ta có AD cố định nên điểm K cố định.
Trong ∆ ABD ta có:
IB = ID (tính chất hình bình hành)
KA = KD (theo cách vẽ)
nên KI là đường trung bình của ∆ ABD
⇒ KI = \(\dfrac{1}{2}AB=\dfrac{1}{2}.2\) = 1 (cm) (tính chất đường trung bình của tam giác)
B và C thay đổi thì I thay đổi luôn cách điểm K cố định một khoảng không đổi nên I chuyển động trên (K ; 1 cm)

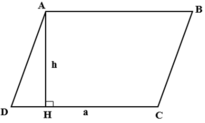
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8 c m 2 .
Chọn đáp án B.

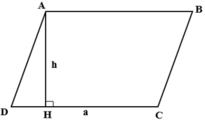
Ta có : S = a.h
Khi đó ta có: S = 4.2 = 8 c m 2 .
Chọn đáp án B.

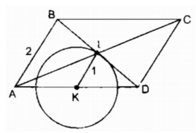
Gọi K là trung điểm của cạnh AD.
ta có AD cố định nên điểm K cố định.
Trong ∆ ABD ta có:
IB = ID (tính chất hình bình hành)
KA = KD (theo cách vẽ)
nên KI là đường trung bình của ∆ ABD
⇒ KI = 1/2 AB = 1/2.2 = 1 (cm) (tính chất đường trung bình của tam giác)
B và C thay đổi thì I thay đổi luôn cách điểm K cố định một khoảng không đổi nên I chuyển động trên (K; 1 cm)

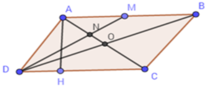
SABCD = AH.CD = 4.3 = 12(cm2)
Vì M là trung điểm của AB nên AM = 1 2 AB = 1 2 .4 = 2(cm)
Ta có chiều cao từ đỉnh D đến cạnh AM của tam giác ADM bằng chiều cao AH của hình bình hành.
=> SADM = 1 2 AH.AM = 1 2 .3.2 = 3(cm2)
Đáp án cần chọn là: A

Giải thích các bước giải:
Gọi AH là đg cao từ A xuống cạnh CD
a, diện h hbh=AHxCD=12.16=192
b,M trung điểm AB nên AM=16:2=8cm
vì ABCD là hbh nên đường cao từ D xuống AB= AH=12cm
do đó diện tích tam giác ADM=12x8:2=48
c, Xét tam giác ANM và CND
vì AM//CD nên CDAM=DNMN=12CDAM=DNMN=12 suy ra DN=2NM
d, vì DN=2NM nên chiều cao từ D xuống AM = 3 từ N xuống AM=> chiều cao từ N xuống AM=12:3=4cm
suy ra diện tích AMN=AMx4:2=16
a) Phần thuận
Gọi O là điểm đối xứng với D qua C thì O là một điểm cố định
Tứ giác ABOC có AB // OC; AB = OC (vì cùng bằng CD) nên ABOC là hình bình hành
⟹ OB = AC = 2cm. Điểm B cách điểm O cố định một khoảng 2cm nên điểm B nằm trên đường tròn tâm O bán kính 2cm.
Giới hạn: Vì B, C, D không thẳng hàng nên B nằm trên đường tròn tâm O bán kính 2cm trừ giao điểm của đường tròn này với đường thẳng CD.
b) Phần đảo
Lấy điểm B bất kì trên đường tròn tâm O bán kính 2cm (trừ giao điểm của đường tròn này với đường thẳng CD). Suy ra OB = 2cm. Vẽ hình bình hành ABCD. Ta chứng minh hình bình hành có AC = 2cm
Thật vậy, AB // CD và AB = CD ⟹ AB // CO và AB = CO. Do đó tứ giác ABOC là hình bình hành, suy ra AC = OB = 2cm
c) Kết luận
Vậy quỹ tích của điểm B là đường tròn tâm O bán kính 2cm, trừ giao điểm của đường tròn này với đường thẳng CD.