Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét hai tam giác AEB và DEC có:
\(\widehat {BAC} = \widehat {C{\rm{D}}B}\)(giả thiết)
\(\widehat {AEB} = \widehat {DEC}\) (đối đỉnh)
Suy ra \(\Delta A{\rm{E}}B \backsim \Delta DEC\) suy ra: \(\frac{{A{\rm{E}}}}{{DE}} = \frac{{BE}}{{CE}} \Rightarrow \frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
Xét hai tam giác AED và BEC có:
\(\widehat {A{\rm{ED}}} = \widehat {BEC}\) (đối đỉnh)
\(\frac{{A{\rm{E}}}}{{BE}} = \frac{{DE}}{{CF}}\)
Suy ra ΔAED ∽ ΔBEC (g – c – g)

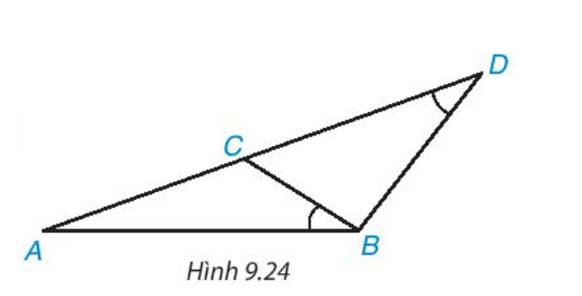
Xét tam giác ABC và tam giác ADB có
\(\widehat {ABC} = \widehat {A{\rm{D}}B}\) và \(\widehat A\) chung
=> ΔABC ∽ ΔADB (g.g)
=> \(\frac{{AB}}{{AD}} = \frac{{AC}}{{AB}}\)
=> \(A{B^2} = A{\rm{D}}.AC\)

Xét \(\Delta ABD\)có: \(\widehat {BAD} + \widehat {ABD} + \widehat {BDA} = {180^0}\)
Xét \(\Delta BCD\)có: \(\widehat {BCD} + \widehat {BDC} + \widehat {DBC} = {180^0}\)
\(\begin{array}{l} \Rightarrow \widehat {BAD} + \widehat {ABD} + \widehat {BDA} = \widehat {BCD} + \widehat {BDC} + \widehat {DBC}\\ \Rightarrow \widehat {DAB} = \widehat {DBC}(do\,\widehat {BAD} = \widehat {BCD};\widehat {ABD} = \widehat {BDC})\end{array}\)
Xét \(\Delta ABD\) và \(\Delta CDB\) có:
\(\begin{array}{l}\left. \begin{array}{l}\widehat {ABD} = \widehat {CDB}\\BDchung\\\widehat {DBA} = \widehat {DBC}\end{array} \right\} \Rightarrow \Delta ABD = \Delta CDB(g.c.g)\\ \Rightarrow AB = DC\\AD = CB\end{array}\)
Suy ra tứ giác ABCD là hình bình hành vì có cặp cạnh đối bằng nhau

a, Tứ giác ABCD có:
\(\widehat {ABC} + \widehat {BCD} + \widehat {CDA} + \widehat {DAB} = {360^0}\)
\(\widehat {ABC} + \widehat {DAB} + \widehat {ABC} + \widehat {DAB} = {360^0}\)(do \(\widehat {DAB} = \widehat {BCD};\widehat {ABC} = \widehat {CDA}\))
\(\begin{array}{l}2\widehat {ABC} + 2\widehat {DAB} = {360^0}\\\widehat {ABC} + \widehat {DAB} = \dfrac{{{{360}^0}}}{2} = {180^0}\end{array}\)
b, Ta có: \(\widehat {xAD} + \widehat {DAB} = {180^0}\)(do tia Ax là tia đối của tia AB)
Nên
\(\begin{array}{l}\widehat {xAD} + \widehat {DAB} = \widehat {ABC} + \widehat {DAB}\\ \Rightarrow \widehat {xAD} = \widehat {ABC}\end{array}\)
Suy ra AD//BC (hai góc đồng vị bằng nhau)
c, Vì AD//BC \( \Rightarrow \widehat {ADB} = \widehat {DBC}\) (2 góc so le trong)
Xét \(\Delta A{\rm{D}}B\) có \(\widehat {ABD} = {180^0} - \widehat {ADB} - \widehat {DAB} = {180^0} - \widehat {DBC} - \widehat {BCD}\left( 1 \right)\)
( vì \(\widehat {ADB} = \widehat {DBC};\widehat {DAB} = \widehat {BCD})\)
Xét \(\Delta CDB\) có: \(\widehat {BDC} = {180^0} - \widehat {DBC} - \widehat {BCD}\left( 2 \right)\)
Từ (1), (2) suy ra \(\widehat {ABD} =\widehat {BDC}\)
Xét \(\Delta ADB\) và \(\Delta BCD\)có:
\(\left. \begin{array}{l}DBchung\\\widehat {ABD} = \widehat {BDC}\\\widehat {ABD} = \widehat {DBC}\end{array} \right\} \Rightarrow \Delta A{\rm{D}}B = \Delta C{\rm{D}}B \Rightarrow A{\rm{D}} = BC,AB = CB\)
Suy ra tứ giác ABCD có cặp cạnh đối bằng nhau nên ABCD là hình bình hành.

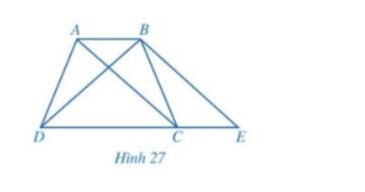
Do ABCD là hình thang nên AB//CD.
Kẻ BE//AC, \(E \in CD\) nên CE//AB.
\( \Rightarrow \widehat {BCE} = \widehat {ABC}\); \(\widehat {CBE} = \widehat {ACB}\) (hai góc so le trong).
a, Xét \(\Delta ABC\)và \(\Delta ECB\) có:
\(\widehat {BCE} = \widehat {ABC}\)
BC chung
\(\widehat {CBE} = \widehat {ACB}\) (do BC//AC )
\( \Rightarrow \Delta ABC = \Delta ECB\)(g.c.g)
b, BE = AC = BD
\( \Rightarrow \Delta BDE\)cân tại B
\( \Rightarrow \widehat {BDE} = \widehat {BED}\)
Do \(\Delta ABC = \Delta ECB\)
\( \Rightarrow \widehat {BEC} = \widehat {BAC}\) (2 góc tương ứng) hay \(\widehat {BED} = \widehat {BAC}(1)\)
Mà: \(\widehat {BAC} = \widehat {ACD}\) (do AB//CD) (2)
Từ (1), (2) suy ra: \(\widehat {BED} = \widehat {ACD}\)
c, Theo câu b:
\(\begin{array}{l}\widehat {BED} = \widehat {BDE}\\\widehat {ACD} = \widehat {BED}\end{array}\) suy ra: \(\widehat {ACD} = \widehat {BDE}\) hay \(\widehat {ACD} = \widehat {BDC}\)
Xét \(\Delta ACD\)và \(\Delta BDC\)có:
CD chung
\(\widehat {ACD} = \widehat {BDC}\)
AC = BD (gt)
\( \Rightarrow \Delta ACD = \Delta BDC(c.g.c)\)
\( \Rightarrow \widehat {ADC} = \widehat {BCD}\) (2 góc tương ứng)
d, Hình thang ABCD (AB//CD) có \(\widehat {ADC} = \widehat {BCD}\)nên hình thang ABCD là hình thang cân.

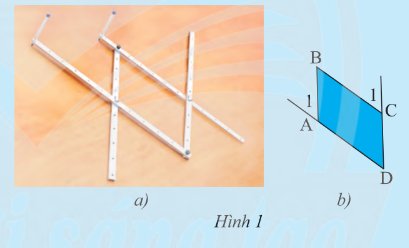
Sau khi đo, ta thấy bốn góc \(\widehat {\rm{A}}\), \(\widehat {\rm{B}}\), \(\widehat {\rm{C}}\), \(\widehat {\rm{D}}\) có số đo bằng nhau và bằng \(90^\circ \)

Sau khi đo góc ta thấy cặp góc \(\widehat {{A_1}}\) và \(\widehat {\rm{D}}\), \(\widehat {{{\rm{C}}_{\rm{1}}}}\) và \(\widehat {\rm{D}}\) bằng nhau
Mà các góc ở vị trí đồng vị
Suy ra: \(AB\) // \(CD\); \(AD\) // \(BC\)

Câu hỏi của headsot96 - Toán lớp 8 - Học toán với OnlineMath
Em tham khảo!

a) Vì ABCD là hình bình hành nên AB // CD; AD // BC.
Suy ra \(\widehat {BAC} = \widehat {AC{\rm{D}}};\widehat {BCA} = \widehat {DAC}\)(hai góc so le trong).
Xét ∆ABC và ∆CDA có:
\(\widehat {BAC} = \widehat {AC{\rm{D}}}\) (chứng minh trên);
Cạnh AC chung.
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó ∆ABC = ∆CDA (g.c.g).
Suy ra AB = CD, AD = BC (các cặp cạnh tương ứng); \(\widehat {ABC} = \widehat {C{\rm{D}}A}\) (hai góc tương ứng).
b) Xét ∆ABD và ∆CDB có:
AB = CD (chứng minh trên);
AD = BC (chứng minh trên);
Cạnh BD chung.
Do đó ∆ABD = ∆CDB.
Suy ra \(\widehat {DAB} = \widehat {BC{\rm{D}}}\) (hai góc tương ứng).
c) Xét ∆AOB và ∆COD có:
\(\widehat {BAC} = \widehat {AC{\rm{D}}}\) (chứng minh trên);
AB = CD (chứng minh trên);
\(\widehat {BCA} = \widehat {DAC}\) (chứng minh trên);
Do đó ∆AOB = ∆COD (g.c.g).
Suy ra OA = OC, OB = OD (các cặp cạnh tương ứng).


- Xét tam giác ABD và tam giác ACE có \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\), góc A chung
=> ΔABD ∽ ΔACE (g.g)
- Vì ΔABD ∽ ΔACE
=> \(\widehat {A{\rm{D}}B} = \widehat {A{\rm{E}}C}\)
=> \(\widehat {C{\rm{D}}O} = \widehat {BEO}\) (1)
- Có \(\widehat {AB{\rm{D}}} = \widehat {AC{\rm{E}}}\)
Mà \(\widehat {AB{\rm{D}}} + \widehat {EBO} = {180^o}\)
\(\widehat {AC{\rm{E}}} + \widehat {DCO} = {180^o}\)
=> \(\widehat {EBO} = \widehat {DCO}\) (2)
Từ (1) và (2) => ΔBOE ∽ ΔCOD (g.g)