Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
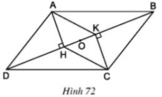
a)+ ABCD là hình bình hành
⇒ AD // BC và AD = BC.
⇒ ∠ADH = ∠CBK (Hai góc so le trong).
Hai tam giác vuông AHD và CKB có:
AD = BC
∠ADH = ∠CBK
⇒ ΔAHD = ΔCKB (cạnh huyền, góc nhọn)
⇒ AH = CK
+ AH ⊥ BD; CK ⊥ BD ⇒ AH // CK
Tứ giác AHCK có AH // CK, AH = CK nên là hình bình hành.
b) Hình bình hành AHCK có O là trung điểm HK
⇒ O = AC ∩ HK ⇒ A, C, O thẳng hàng.
a) Hai tam giác vuông AHD và CKD có:
AD = CB (gt)
= 
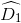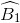(so le trong)
Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)
Suy ra AH = CK
Tứ giác AHCK có AH Vuông góc với DB và CK cũng vuông góc với DB. Nên AH // CK, Mà theo chứng mình trên AH = CK nên là hình bình hành,
b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.
Tham khảo thôi!
a) Hai tam giác vuông AHD và CKD có:
AD = CB (gt)
\(\widehat{D_1}\) = \(\widehat{B_1}\) (so le trong)
Nên ∆AHD = ∆CKB (cạnh huyền, góc nhọn)
Suy ra AH = CK
Tứ giác AHCK có AH Vuông góc với DB và CK cũng vuông góc với DB. Nên AH // CK, Mà theo chứng mình trên AH = CK nên là hình bình hành,
b) Xét hình bình hành AHCK, trung điểm O của đường chéo của hình bình hành). Do đó ba điểm A, O, C thẳng hàng.
b) Xét hai tam giác vuông AHD và CKB có:
AD=BC
góc ADB=góc DBC (so le trong).
=> tam giác AHD=tam giác CKB (ch-gn)
=> BH=CK( hai cạnh tương ứng)
Lấy M trung điểm BD , nên MD=MB => MD-DH=MB-BK=> MH=MK, nên M Trung điểm HK
Vì ABCD là hình bình hành nên AC cắt BD tại trung điểm M.
Hay M là Trung điểm AC, mà M trung điểm HK.
Nên AKCH là hình bình hành.
A H K B C D I F
1/
Ta có
\(ÁH\perp BD\left(gt\right);CK\perp BD\left(gt\right)\) => AH//CK (1)
Xét tg vuông ADH và tg vuông BCK có
AD//BC (cạnh đối hbh) \(\Rightarrow\widehat{ADH}=\widehat{CBK}\) (góc so le trong)
AD=BC (cạnh đối hbh)
=> tg ADH = tg BCK (Hai tg cuông có cạnh huyền và góc nhọn tương ứng bằng nhau) => AH=CK (2)
Từ (1) và (2) => AHCK là hbh (Tứ giác có 1 cặp cạnh đối // và = nhau là hbh)
2/
Ta có
AH//CK (cmt) => AI//CF
AB//CD (cạnh đối hbh) => AF//CI
=> AICF là hbh (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh) => AI = CF (cạnh đối hbh)
4/ Xét hbh AHCK có
AC cắt HK tại O' => O'H=O'K (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường) => O' là trung điểm HK
Mà O cũng là trung điểm HK
=> \(O\equiv O'\) => A; O; C thẳng hàng
5/
Xét hbh AHCK có
AC cắt HK tại O (cmt) => OA=OC
Xét hbh ABCD có
OA=OC (cmt) => OB=OD (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Ta có
AICF là hbh (cmt) => FI cắt AC tại trung điểm O của AC (trong hbh 2 đường chéo cắt nhau tại trung điểm mỗi đường)
=> AC; BD; IF đồng quy
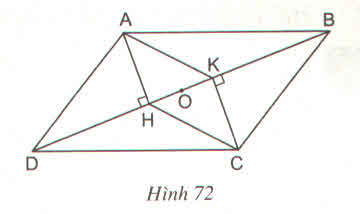
Hình đâu ạ?
SGK lớp 8, tập 1, hình học. Giúp mình nha