Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét tam giác \(ABC\) có \(DE//BC\) nên theo định lí Thales ta có:
\(\frac{{AD}}{{BD}} = \frac{{AE}}{{EC}} \Rightarrow \frac{x}{2} = \frac{6}{3}\). Do đó, \(x = \frac{{6.2}}{3} = 4\).
Vậy \(x = 4\).

Ta có tam giác ABC ~ tam giác MNP
\(\dfrac{AB}{MN}=\dfrac{AC}{MP}\Rightarrow MP=\dfrac{AC.MN}{AB}=\dfrac{15}{2}cm\)

Vì ΔABC đồng dạng với ΔMNP nên A B M N = A C M P = B C N P hay 5 10 = A C 5 = 6 N P
=> AC = 5.5 10 = 2,5; NP = 6.10 5 = 12
Vậy NP = 12cm, AC = 2,5cm
Đáp án: A
Chọn D
Chọn đáp án D
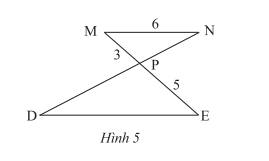
Ta có: \(ME = MP + PE = 3 + 5 = 8\)
Xét tam giác \(PDE\) có \(MN//DE\), theo hệ quả của định lí Thales ta có:
\(\frac{{MP}}{{PE}} = \frac{{MN}}{{DE}} \Leftrightarrow \frac{3}{5} = \frac{6}{{DE}} \Rightarrow DE = \frac{{6.5}}{3} = 10\)
Vậy \(DE = 10cm\).