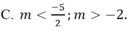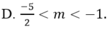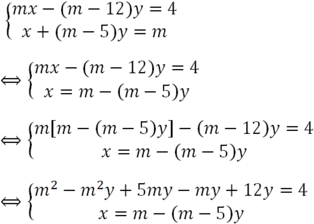Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

m 2 x + m + 4 y = 2 m x + y = 1 − y ⇔ m 2 x + m + 4 y = 2 m x + m + 1 y = 1
Ta có: D = m 2 m + 4 m m + 1 = m 3 − 4 m = m m 2 − 4
D x = 2 m + 4 1 m + 1 = 2 m + 1 − m − 4 = m − 2
D y = m 2 2 m 1 = m 2 − 2 m
Nếu D = 0 ⇔ m m 2 - 4 = 0 ⇔ m = 0 m = ± 2
+) Với m = 0 ⇒ D x ≠ 0 nên hệ phương trình vô nghiệm
+) Với m = 2 ⇒ D x = D y = 0 nên hệ phương trình có vô số nghiệm
+) Với m = - 2 ⇒ D x ≠ 0 nên hệ phương trình vô nghiệm
Vậy với m = 0 hoặc m = - 2 thì hệ phương trình vô nghiệm
Đáp án cần chọn là: A

\(\left\{{}\begin{matrix}mx+\left(m+4\right)y=2\\m\left(x+y\right)=1-y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}mx+\left(m+4\right)y=2\\mx+\left(m+1\right)y=1\end{matrix}\right.\)
Nếu \(m=0\), hệ trở thành \(\left\{{}\begin{matrix}4y=2\\y=1\end{matrix}\right.\Rightarrow\) vô nghiệm
\(\Rightarrow m=0\left(tm\right)\)
Nếu \(m=-1\), hệ trở thành \(\left\{{}\begin{matrix}-x+3y=2\\-x=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=\dfrac{1}{3}\end{matrix}\right.\)
\(\Rightarrow m=-1\left(l\right)\)
Nếu \(m\ne0,m\ne-1\), yêu cầu bài toán thỏa mãn khi \(1=\dfrac{m+4}{m+1}\ne2\)
\(\Rightarrow\) không tồn tại m thỏa mãn
Vậy \(m=0\)

Ta tính các định thức:
D = m 1 1 m = m 2 - 1 = m + 1 . m - 1 ; D x = m + 1 1 2 m = m 2 + m - 2 = m - 1 . m + 2 ; D y = m m + 1 1 2 = m - 1
Xét D = 0 tức là m = 1 hoặc m = -1.
* Nếu m = 1 thì D = Dx = Dy = 0 nên hệ phương trình đã cho có vô số nghiệm.
Do đó, a= 1.
* Nếu m = -1 thì D = 0 nhưng D x ≠ 0 nên hệ phương trình đã cho vô nghiệm.
Do đó, b = -1
Tổng a+ b = 0.
Chọn A.

* Ta có: D = m 1 1 m = m 2 - 1 ; D x = m 1 m m = m 2 - m
Để hệ phương trình đã cho vô nghiệm thì:
D = m 2 - 1 = 0 D x = m 2 - m ≠ 0 ⇔ m = ± 1 m ≠ 0 ⇔ m = - 1 m ≠ 1
Vậy hệ vô nghiệm khi m = -1, vậy chọn đáp án là C.

Xét hệ phương trình: m x − ( m + 1 ) y = 3 m x − 2 m y − m + 2
Ta có: D = m − ( m + 1 ) 1 − 2 m = − 2 m 2 + m + 1 = 2 m + 1 1 − m
D x = 3 m − ( m + 1 ) m + 2 − 2 m = − 6 m 2 + ( m + 2 ) ( m + 1 ) = − 5 m 2 + 3 m + 2 = 5 m + 2 1 − m
D y = m 3 m 1 m + 2 = m 2 + 2 m − 3 m = m 2 − m = m ( m − 1 )
Hệ phương trình có nghiệm duy nhất
⇔ D ≠ 0 ⇔ 2 m + 1 1 − m ≠ 0 ⇔ m ≠ − 1 2 m ≠ 1
Khi đó: x = D x D = 5 m + 2 1 − m 2 m + 1 1 − m = 5 m + 2 2 m + 1 y = D y D = m 1 − m 2 m + 1 1 − m = − m 2 m + 1
Thay giá trị của x, y vào phương trình: x + 2 y = 4 ta được:
5 m + 2 2 m + 1 − 2 m 2 m + 1 = 4 ⇔ 3 m + 2 2 m + 1 = 4 ⇔ 3 m + 2 = 8 m + 4
⇔ m = − 2 5
Đáp án cần chọn là: D

Hệ: m x + 3 m − 2 y + m − 3 = 0 2 x + m + 1 y − 4 = 0 ⇔ m x + 3 m − 2 y = 3 − m 2 x + m + 1 y = 4
Ta có:
D = m 3 m − 2 2 m + 1 = m 2 − 5 m + 4 = m − 1 m − 4
D x = 3 − m 3 m − 2 4 m + 1
= 3 − m m + 1 − 4 3 m − 2 = − m + 11 = 1 − m m + 11
D y = m 3 − m 2 4 = 4 m − 6 + 2 m = 6 m − 6 = 6 m − 1
Hệ phương trình có nghiệm duy nhất
⇔ D ≠ 0 ⇔ m − 1 m − 4 ≠ 0 ⇔ m ≠ 1 m ≠ 4
⇒ x = D x D = 1 − m m + 11 m − 1 m − 4 = m + 11 4 − m ( 1 ) y = D y D = 6 m − 1 m − 1 m − 4 = 6 m − 4 ( 2 )
Từ 2 ⇒ m − 4 y = 6 ⇔ m y = 6 + 4 y ⇔ m = 6 + 4 y y = 6 y + 4
Thay vào (1) ta được:
x = 6 y + 4 + 11 : 4 − 6 y − 4 = − 6 + 15 y 6 = − 1 − 15 6 y
Đáp án cần chọn là: C